Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Uma equipe de pesquisadores coleta e publica informações detalhadas sobre fatores que afetam doenças cardíacas. As variáveis incluem idade, sexo, níveis de colesterol, frequência cardíaca máxima e muito mais. Este exemplo é baseado em um conjunto de dados públicos que fornece informações detalhadas sobre doenças cardíacas. Os dados originais são de archive.ics.uci.edu.
Após a exploração inicial com Classificação CART® para identificar os preditores importantes, os pesquisadores usam Classificação TreeNet® e Classificação Random Forests® para criar modelos mais aprofundados a partir do mesmo conjunto de dados. Os pesquisadores comparam a tabela de sumário do modelo e o gráfico ROC dos resultados para avaliar qual modelo proporciona um resultado de predição melhor. Para os resultados das demais análises, vá para Exemplo de Classificação CART® e Exemplo de Classificação Random Forests®.
- Abra os dados amostrais, BinarioDeDoencasCardiacas.MWX.
- Selecione .
- Na lista suspensa, selecione Resposta binária.
- Em Resposta, digite 'Doença cardíaca'.
- Em Evento de resposta, selecione Sim para indicar que a doença cardíaca foi identificada no paciente.
- Em Preditores contínuos, digite Idade, 'Pressão Arterial de descanso', Colesterol, 'Max Heart Rate', e 'Pico Antigo'.
- Em Preditores categóricos, digite Sexo, 'Tipo de dor torácica', 'Açúcar no sangue em jejum', 'Resto ECG', 'Exercício Angina', Inclinação, 'Principais Navios', e Thal.
- Clique em OK.
Interpretar os resultados
Para esta análise, o Minitab cultiva 300 árvores e o número ótimo de árvores é de 298. Como o número ótimo de árvores está próximo ao número máximo de árvores cultivadas pelo modelo, os pesquisadores repetem a análise com mais árvores.
Sumário do modelo
| Preditores totais | 13 |
|---|---|
| Preditores importantes | 13 |
| Número de árvores cultivadas | 300 |
| Número ótimo de árvores | 298 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| -Log da Verossimilhança Média | 0,2556 | 0,3881 |
| Área sob a curva ROC | 0,9796 | 0,9089 |
| IC de 95% | (0,9664; 0,9929) | (0,8759; 0,9419) |
| Elevação | 2,1799 | 2,1087 |
| Taxa de classificação errada | 0,0891 | 0,1617 |
Exemplo com 500 árvores
- Selecione Ajustar hiperparâmetros nos resultados.
- Em Número de árvores, insira 500.
- Clique em Exibir resultados.
Interpretar os resultados
Para esta análise, foram cultivadas 500 árvores e o número ótimo de árvores é de 351. O melhor modelo usa uma taxa de aprendizado de 0,01, usa uma fração de subamostra de 0,5 e usa 6 como o número máximo de nós terminais.
Método
| Critério para seleção do número ótimo de árvores | Log-verossimilhança máximo |
|---|---|
| Validação do modelo | Validação cruzada de 5 dobras |
| Taxa de aprendizado | 0,01 |
| Método de seleção da subamostra | Completamente aleatório |
| Fração da subamostra | 0,5 |
| Nós máximos terminais por árvore | 6 |
| Tamanho mínimo do nó terminal | 3 |
| Número de preditores selecionados para divisão de nós | Número total de preditores = 13 |
| Linhas usadas | 303 |
Informações de resposta binária
| Variável | Classe | Contagem | % |
|---|---|---|---|
| Doença cardíaca | Sim (Evento) | 139 | 45,87 |
| Não | 164 | 54,13 | |
| Todos | 303 | 100,00 |
Método
| Critério para seleção do número ótimo de árvores | Log-verossimilhança máximo |
|---|---|
| Validação do modelo | Validação cruzada de 5 dobras |
| Taxa de aprendizado | 0,001; 0,01; 0,1 |
| Fração da subamostra | 0,5; 0,7 |
| Nós máximos terminais por árvore | 6 |
| Tamanho mínimo do nó terminal | 3 |
| Número de preditores selecionados para divisão de nós | Número total de preditores = 13 |
| Linhas usadas | 303 |
Informações de resposta binária
| Variável | Classe | Contagem | % |
|---|---|---|---|
| Doença cardíaca | Sim (Evento) | 139 | 45,87 |
| Não | 164 | 54,13 | |
| Todos | 303 | 100,00 |
Otimização de hiperparâmetros
| Modelo | Número ótimo de árvores | -Log da Verossimilhança Média | Área sob a curva ROC | Taxa de classificação errada | Taxa de aprendizado | Fração da subamostra |
|---|---|---|---|---|---|---|
| 1 | 500 | 0,542902 | 0,902956 | 0,171749 | 0,001 | 0,5 |
| 2* | 351 | 0,386536 | 0,908920 | 0,175027 | 0,010 | 0,5 |
| 3 | 33 | 0,396555 | 0,900782 | 0,161694 | 0,100 | 0,5 |
| 4 | 500 | 0,543292 | 0,894178 | 0,178142 | 0,001 | 0,7 |
| 5 | 374 | 0,389607 | 0,906620 | 0,165082 | 0,010 | 0,7 |
| 6 | 39 | 0,393382 | 0,901399 | 0,174973 | 0,100 | 0,7 |
| Modelo | Máximo de do nós terminais |
|---|---|
| 1 | 6 |
| 2* | 6 |
| 3 | 6 |
| 4 | 6 |
| 5 | 6 |
| 6 | 6 |
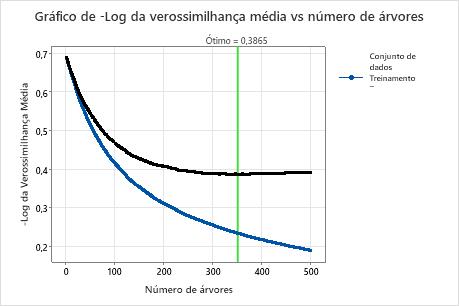
O gráfico de log-verossimilhança médio vs número de árvores mostra toda a curva sobre o número de árvores cultivadas. O valor ótimo para os dados do teste é 0,3865 quando o número de árvores é 351.
Sumário do modelo
| Preditores totais | 13 |
|---|---|
| Preditores importantes | 13 |
| Número de árvores cultivadas | 500 |
| Número ótimo de árvores | 351 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| -Log da Verossimilhança Média | 0,2341 | 0,3865 |
| Área sob a curva ROC | 0,9825 | 0,9089 |
| IC de 95% | (0,9706; 0,9945) | (0,8757; 0,9421) |
| Elevação | 2,1799 | 2,1087 |
| Taxa de classificação errada | 0,0759 | 0,1750 |
Sumário do modelo
| Preditores totais | 13 |
|---|---|
| Preditores importantes | 13 |
| Estatísticas | Out-of-Bag |
|---|---|
| -Log da Verossimilhança Média | 0,4004 |
| Área sob a curva ROC | 0,9028 |
| IC de 95% | (0,8693; 0,9363) |
| Elevação | 2,1079 |
| Taxa de classificação errada | 0,1848 |
A tabela sumário do modelo mostra que a probabilidade média negativa de log-verossimilhança quando o número de árvores é de 351 é aproximadamente 0,23 para os dados de treinamento e é aproximadamente 0,39 para os dados de teste. Essas estatísticas indicam um modelo semelhante ao que o Minitab Random Forests® cria. Além disso, as taxas de classificação errada são semelhantes.
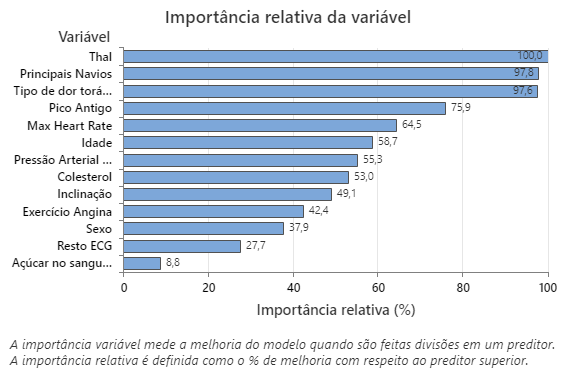
O gráfico de importância relativa da variável representa os preditores por ordem de seu efeito sobre a melhoria do modelo quando as divisões são feitas em um preditor sobre a sequência de árvores. A variável preditora mais importante é o Thal. Se a contribuição da variável preditora superior, Thal, for de 100%, então a próxima variável importante, Vasos principais, tem uma contribuição de 97,8%. Isso significa que os Vasos principais são 97,8% tão importantes quanto Thal neste modelo de classificação.
Matriz de confusão
| Classe predita (Treinamento) | |||||||
|---|---|---|---|---|---|---|---|
| Classe predita (Teste) | |||||||
| Classe real | Contagem | Sim | Não | % Correto | Sim | Não | % Correto |
| Sim (Evento) | 139 | 124 | 15 | 89,21 | 110 | 29 | 79,14 |
| Não | 164 | 8 | 156 | 95,12 | 24 | 140 | 85,37 |
| Todos | 303 | 132 | 171 | 92,41 | 134 | 169 | 82,51 |
| Estatísticas | Treinamento (%) | Teste (%) |
|---|---|---|
| Taxa de positivo verdadeiro (sensibil. ou poder) | 89,21 | 79,14 |
| Taxa de positivo falso (erro tipo I) | 4,88 | 14,63 |
| Taxa de negativo falso (erro tipo II) | 10,79 | 20,86 |
| Taxa de negativo verdadeiro (especificidade) | 95,12 | 85,37 |
A matriz confusão mostra se o modelo separa as classes bem e corretamente. Neste exemplo, a probabilidade de um evento ser predito corretamente é de 79,14%. A probabilidade de que um não evento ser predito corretamente é de 85,37%.
Classificação errada
| Treinamento | Teste | ||||
|---|---|---|---|---|---|
| Classificado errado | % de erro | Classificado errado | % de erro | ||
| Classe real | Contagem | ||||
| Sim (Evento) | 139 | 15 | 10,79 | 29 | 20,86 |
| Não | 164 | 8 | 4,88 | 24 | 14,63 |
| Todos | 303 | 23 | 7,59 | 53 | 17,49 |
A taxa de classificação errada ajuda a indicar se o modelo irá predizer novas observações com exatidão. Para predição de eventos, o erro de classificação errada do teste é de 20,86%. Para a predição de não evento, o erro de classificação incorreta é de 14,63% e, no geral, o erro de classificação incorreta é de 17,49%.
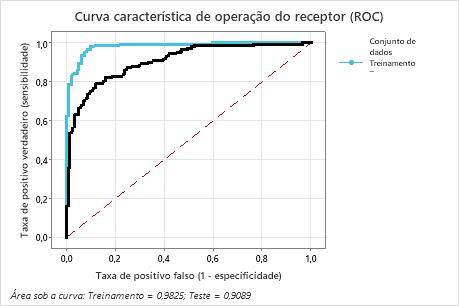
A área sob a curva ROC quando o número de árvores é 351 é aproximadamente 0,98 para os dados de treinamento e é aproximadamente 0,91 para os dados de teste. Isso mostra uma boa melhora em relação ao modelo de Classificação CART®. O modelo Classificação Random Forests® tem um teste AUROC de 0,9028, de modo que esses dois métodos produzem resultados semelhantes.
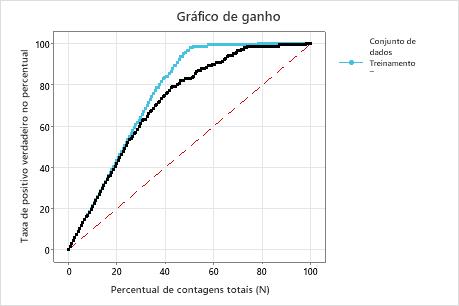
Neste exemplo, o gráfico de ganho mostra um aumento acentuado acima da linha de referência, em seguida, um achatamento. Neste caso, aproximadamente 40% dos dados representam aproximadamente 80% dos positivos verdadeiros. Essa diferença é o ganho extra com o uso do modelo.
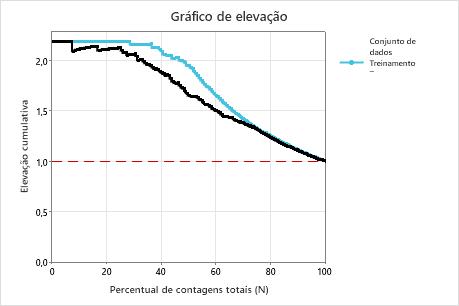
Neste exemplo, o gráfico de elevação mostra um grande aumento acima da linha de referência que cai gradualmente.
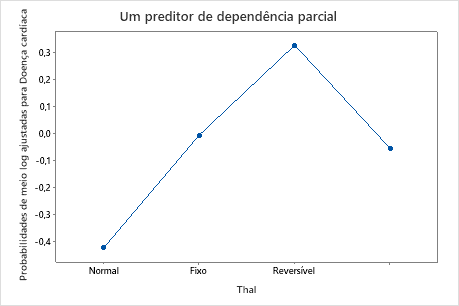
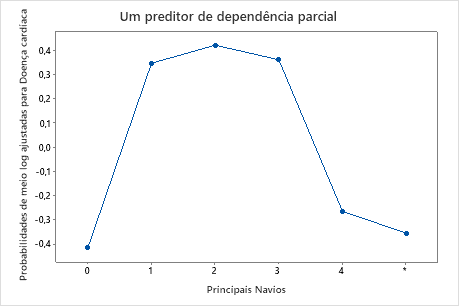
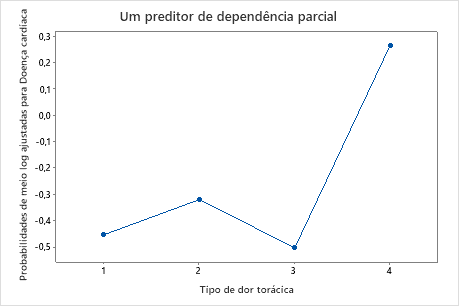
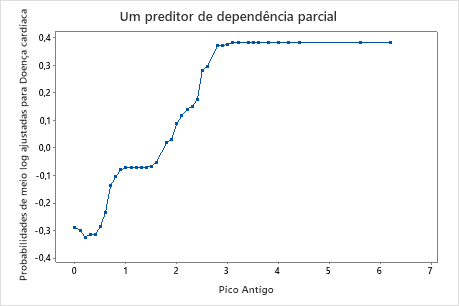
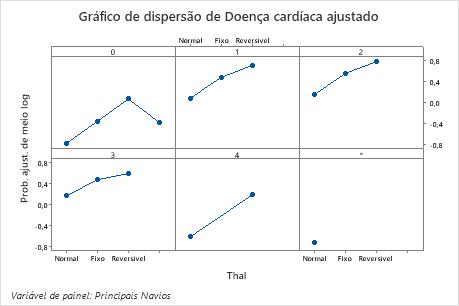
Use os gráficos de dependência parcial para obter uma visão de como as variáveis importantes ou pares de variáveis afetam a resposta predita. Os valores de resposta na escala de meio log são as predições oriundas do modelo. Os gráficos de dependência parcial mostram se a relação entre a resposta e uma variável é linear, monotônica ou mais complexa.
Por exemplo, no gráfico de dependência parcial que traça o tipo de dor torácica, as chances de meio log variam, e depois aumentam vertiginosamente. Quando o tipo de dor torácica é 4, as chances de meio log da incidência de doenças cardíacas aumentam de aproximadamente −0,04 para 0,03. Selecione ou para produzir gráficos para outras variáveis