Tabela Sumário do modelo para Regressão Random Forests^®

R² é a porcentagem de variação na resposta que o modelo explica.

Interpretação

Use o R² para determinar se o modelo ajusta bem seus dados. Quanto maior o valor R², melhor o modelo ajusta seus dados. R² está sempre entre 0% e 100%.

Você pode ilustrar graficamente o significado de diferentes valores de R². O primeiro gráfico ilustra um modelo de regressão simples que explica 85,5% da variação na resposta. O segundo gráfico ilustra um modelo que explica 22,6% da variação da resposta. Quanto mais variação for explicada pelo modelo, mais perto dos valores ajustados caem os pontos de dados. Teoricamente, se um modelo puder explicar 100% da variação, os valores ajustados sempre equivaleriam aos valores observados e todos os pontos de dados cairiam sobre a linha y = x.

Observação

Como a Random Forests® usa dados out-of-bag para calcular R², mas não para se adequa ao modelo, o excesso de adaptação do modelo não é uma preocupação.

A raiz do quadrado médio do erro (RMSE) mede a exatidão do modelo. Os outliers exercem um efeito maior sobre o RMSE do que sobre o MAD e o MAPE.

O erro quadrado médio (MSE) mede a exatidão do modelo. Os outliers exercem um efeito maior sobre o MSE do que sobre o MAD e o MAPE.

O desvio absoluto médio (MAD) expressa exatidão nas mesmas unidades que os dados, o que ajuda a conceituar a quantidade de erro. Os outliers têm menos efeito sobre o MAD do que sobre o R², RMSE e MSE.

O erro percentual absoluto médio (MAPE) expressa o tamanho do erro em relação ao tamanho do valor de resposta. Assim, o mesmo erro de tamanho terá um valor MAPE maior para um valor menor da variável de resposta do que para um valor maior. Como o MAPE é um percentual, pode ser mais fácil de entender do que a outra estatística de medida de exatidão. Por exemplo, se o MAPE, em média, é de 0,05, então a relação média entre o erro ajustado e o valor real em todos os casos é de 5%. Os outliers têm menos efeito sobre o MAPE do que sobre o R², RMSE e MSE.

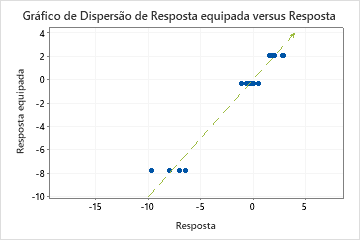
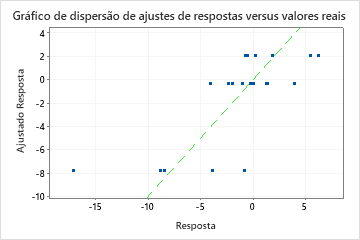
No entanto, às vezes você pode ver um valor MAPE muito grande, mesmo que o modelo pareça ajustar bem os dados. Examine o gráfico de valor de resposta ajustado versus real para ver se algum dos valores de dados estão próximos de 0. Como o MAPE divide o erro absoluto pelos dados reais, os valores próximos a 0 podem inflar muito o MAPE.