Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Variáveis importantes
O Minitab Statistical Software oferece dois métodos para classificar a importância das variáveis.
Permutação
- A = 87
- B = 9
- C = 4
Em seguida, a margem para essa linha é de 0,87 - 0,09 = 0,78.
A margem média out-of-bag é a margem média para todas as linhas de dados.
Para determinar a importância da variável, permute aleatoriamente os
valores de uma variável,
xm através dos dados out-of-bag. Deixe os valores de
resposta e os outros valores do preditor iguais. Em seguida, use os mesmos
passos para calcular a margem média dos dados permutados, 
.
A importância para a variável xm vem da diferença das duas médias:
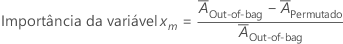
em que 
é a margem média antes da permutação. O Minitab arredonda valores menores que
10–7 para 0.
Gini
Qualquer árvore de classificação é uma coleção de divisões. Cada divisão proporciona melhorias à árvore.
A fórmula a seguir fornece a melhoria em um único nó:
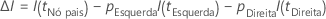
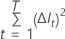
em que 
é o número
de nódulos que se dividem e 
para
qualquer nó 
em que a
variável de interesse não é o divisor.
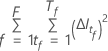
Em que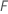 
é o número de
árvores na floresta e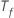
é o número de nódulos que se dividem em árvore 
.
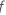O cálculo da impureza do nó é semelhante ao método de Gini. Para obter detalhes sobre o método de Gini, vá para Métodos de divisão de nós em Classificação CART®.
Média − Log-verossimilhança
Dados out-of-bag
O cálculo usa as amostras out-of-bag de cada árvore da floresta. Devido à natureza das amostras out-of-bag, espere usar diferentes combinações de árvores para encontrar a contribuição para a probabilidade de registro para cada linha nos dados.
Para uma determinada árvore na floresta, um voto de classe para uma linha nos dados out-of-bag é a classe predita para a linha da única árvore. A classe predita para uma linha em dados out-of-bag é a classe com o maior voto em todas as árvores da floresta. A probabilidade de classe predita para uma linha nos dados out-of-bag é a razão do número de votos para a classe e o total de votos para a linha. Os cálculos de probabilidade seguem essas probabilidades:
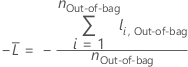
em que
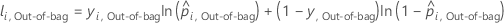
e 
é a probabilidade de evento calculada para a linha
i nos dados out-of-bag.
Notação para dados out-of-bag
| Termo | Descrição |
|---|---|
| nout-of-bag | número de linhas que estão out-of-bag pelo menos uma vez |
| yi, Out-of-bag | valor de resposta binária do caso i nos dados out-of-bag. yi, out-of-bag = 1 para classe de evento, e 0 de outra forma. |
Conjunto de teste
Para uma determinada árvore na floresta, um voto de classe para uma linha no conjunto de testes é a classe predita para a linha a partir da única árvore. A classe predita para uma linha no conjunto de testes é a classe com o maior voto em todas as árvores da floresta. A probabilidade de classe predita para uma linha no conjunto de teste é a razão do número de votos para a classe e o total de votos para a linha. Os cálculos de probabilidade seguem essas probabilidades:
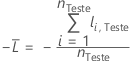
em que
Notação para conjunto de teste
| Termo | Descrição |
|---|---|
| nteste | tamanho amostral do conjunto de teste |
| yi, teste | valor de resposta binária do caso i no conjunto de teste. yi, k = 1 para classe de evento, e 0 de outra forma. |
 | probabilidade de evento previsto para o caso i no conjunto de teste |
Área sob a curva ROC
Fórmula
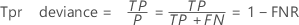
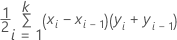
em que k é o número de probabilidades de eventos distintos e (x0, y0) é o ponto (0, 0).
Para calcular a área de uma curva de dados out-of-bag ou um conjunto de teste, use os pontos da curva correspondente.
Notação
| Termo | Descrição |
|---|---|
| Tpr | taxa de positivos verdadeiros |
| FPR | taxa de falsos positivos |
| papel higiênico | positivos verdadeiros, eventos que foram corretamente avaliados |
| fn | falso negativo, eventos que foram avaliados incorretamente |
| P | número de eventos positivos reais |
| Fp | falso positivo, não eventos que foram avaliados incorretamente |
| N | número de eventos negativos reais |
| FNR | taxa de falsos negativos |
| TNR | taxa de negativos verdadeiros |
Exemplo
| x (taxa de falsos positivos) | y (taxa de positivos verdadeiros) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
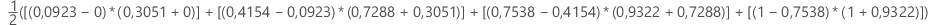
IC de 95% para a área sob a curva ROC
O intervalo a seguir fornece os limites superiores e inferiores para o intervalo de confiança:
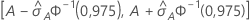
O cálculo do erro padrão da área sob a curva ROC (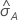
)
vem de Salford Predictive Modeler®. Para obter informações gerais
sobre a estimativa da variância da área sob a curva ROC, consulte as seguintes
referências:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2ª ed.) Heidelberg; Nova York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. e Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., e Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
Notação
| Termo | Descrição |
|---|---|
| A | área sob a curva ROC |
 | 0,975 percentil da distribuição normal padrão |
Ganho
Para ver os cálculos gerais para elevação acumulada, vá para Métodos e fórmulas para o gráfico de Ganho Acumulado para Classificação Random Forests®.
Taxa de classificação errada
A equação a seguir fornece a taxa de classificação errada:
A contagem de classificações incorretas é o número de linhas nos dados out-of-bag em que suas classes preditas são diferentes de suas classes verdadeiras. A contagem total é o número total de linhas nos dados out-of-bag.
Para validação com um conjunto de dados de teste, a contagem de classificações incorretas é a soma de classificações incorretas no conjunto de testes. A contagem total é o número de linhas no conjunto de dados de teste.
