Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Regressão MARS® essencialmente constrói modelos flexíveis ajustando regressões lineares por partes. O modelo tem a restrição de que os pontos finais das linhas por partes se unem uniformemente. Aproximações da não linearidade dos modelos utilizam inclinações de regressão separadas em intervalos distintos dos dados. Uma aproximação do processo é fácil de visualizar no caso simples e 2-dimensional.
No caso 2-dimensional, uma única linha reta se ajusta aos dados. Esse modelo fornece uma linha de base para testar a melhoria da adição de complexidade adicional.
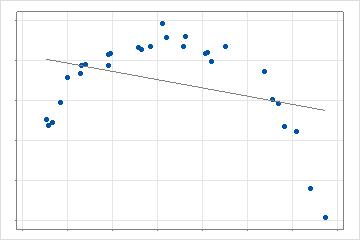
Na próxima etapa, a análise busca o valor de um preditor que cria uma função de base que leva à maior melhoria no critério de busca. O cálculo do critério depende da seleção para a análise e do método de validação. No caso 2-dimensional, este modelo é uma regressão linear por partes com 2 linhas em vez de 1 linha. Com múltiplos preditores, a busca pelo melhor ponto de dados avalia cada preditor que a análise permite.
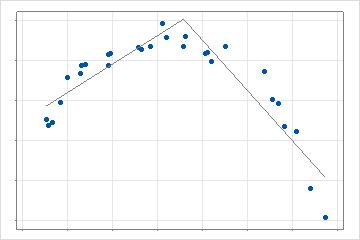
Depois que a análise encontra o primeiro valor que fornece a melhor melhoria, a análise pesquisa os valores preditores restantes para encontrar a melhor melhoria em relação ao modelo atual. No caso 2-dimensional, este modelo tem 3 linhas que descrevem diferentes partes dos dados. A pesquisa repete até o número máximo de funções de base para a análise. Quando as interações são permitidas, a análise executa séries adicionais de pesquisas multiplicando as funções de base candidatas por outras funções de base que já estão presentes no modelo.
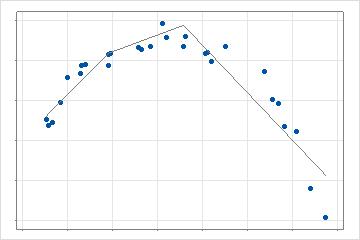
Depois que a análise ajusta rapidamente o número máximo de funções de base e estima os parâmetros dessas funções, a análise identifica o número ideal de funções de base. O número ideal de funções de base usa uma abordagem de eliminação gradual e retrógrada para encontrar o número de funções de base com o melhor valor do critério de otimidade.
Valores ausentes para o ajuste do modelo
Na busca pelas funções de base, Regressão MARS® cria variáveis indicadoras para quaisquer preditores com valores ausentes. A variável indicadora mostra se um valor do preditor está ausente. Se a análise incluir uma função de base para um preditor com valores ausentes no modelo, o modelo também incluirá uma função de base para a variável indicadora. As outras funções de base para o preditor interagem com a função base para a variável indicadora.
Quando um preditor tem um valor ausente, a função base para a variável indicadora anula as outras funções base para esse preditor através da multiplicação por 0. Essas funções de base para valores ausentes estão em todos os modelos em que preditores importantes têm valores ausentes, mesmo modelos aditivos e modelos que desabilitam outros tipos de transformações.
Valores ausentes para previsão
Regressão MARS® calcula as previsões quando os preditores no modelo têm valores ausentes. A análise utiliza diferentes estratégias, dependendo se os valores ausentes para o preditor estavam presentes quando a análise se ajustou ao modelo. Se os valores ausentes para o preditor estiverem presentes quando a análise se ajustar ao modelo, as funções de base no modelo incluirão uma variável indicadora que remove o preditor do modelo quando o preditor tiver um valor ausente.
O segundo caso é quando os valores para predição incluem valores ausentes para um preditor, mas o preditor não tinha valores ausentes quando a análise se ajustava ao modelo. Para calcular previsões neste caso, a análise imputa o valor em falta. Para um preditor contínuo, a média do preditor substitui o valor ausente. Para um preditor categórico, o valor final não ausente no conjunto de dados substitui o valor ausente.
