Neste tópico
Passo 1: Determine se o modelo ajusta bem os dados
- Teste R-quadrado
- Quanto maior o valor R2, melhor o modelo ajusta seus dados. R2 está sempre entre 0% e 100%. Os outliers têm um efeito maior sobre R2 do que sobre o DAM.
- Teste de erro quadrático médio da raiz (RMSE)
- Valores menores indicam um ajuste melhor. Outliers têm um efeito maior no RMSE do que no MAD.
- Teste de erro quadrático médio (MSE)
- Valores menores indicam um ajuste melhor. Outliers têm um efeito maior no MSE do que no MAD.
- Desvio absoluto médio do teste (MAD)
- Valores menores indicam um ajuste melhor. O desvio absoluto médio (MAD) expressa exatidão nas mesmas unidades que os dados, o que ajuda a conceituar a quantidade de erro. Os outliers têm menos efeito sobre o DAM do que sobre o R2, RMSE e MSE.
Sumário do modelo
| Preditores totais | 77 |
|---|---|
| Preditores importantes | 10 |
| Número máximo de funções base | 30 |
| Número ótimo de funções base | 13 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| R-quadrado | 89,61% | 87,61% |
| Raiz do quadrado médio do Erro (RMSE) | 25836,5197 | 27855,6550 |
| Quadrado médio do erro (MSE) | 667525749,7185 | 775937512,8264 |
| Desvio absoluto médio (DAM) | 17506,0038 | 17783,5549 |
Principais resultados: Teste R-quadrado, Teste raiz média erro quadrado (RMSE), Teste médio erro quadrado (MSE), Teste desvio absoluto médio (MAD)
Nestes resultados, o teste R-quadrado é de cerca de 88%. O erro quadrado médio da raiz de teste é de cerca de 27.856. O erro quadrado médio do teste é de cerca de 775.937.513. O desvio absoluto médio do teste é de cerca de 17.784.
Passo 2: Determinar quais variáveis são mais importantes para o modelo
Use o gráfico de importância da variável relativa para ver quais preditores são as variáveis mais importantes para o modelo.
Variáveis importantes estão em pelo menos 1 função base no modelo. A variável com maior pontuação de melhoria é definida como a variável mais importante e as outras variáveis são classificadas de acordo. A importância relativa da variável padroniza os valores de importância para facilitar a interpretação. A importância relativa é definida como a melhoria percentual em relação ao preditor mais importante.
Os valores de importância relativa da variável variam de 0% a 100%. A variável mais importante tem sempre uma importância relativa de 100%. Se uma variável não estiver em uma função base, essa variável não será importante.
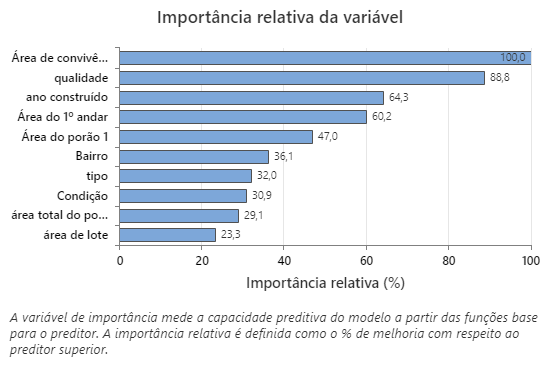
Principal resultado: Importância relativa da variável
- qualidade é cerca de 89% tão importante quanto Área de convivência.
- ano construído é cerca de 64% tão importante quanto Área de convivência.
- Área do 1º andar é cerca de 60% tão importante quanto Área de convivência.
Embora esses resultados incluam 10 variáveis com importância positiva, os rankings relativos fornecem informações sobre quantas variáveis devem ser controladas ou monitoradas para uma determinada aplicação. Quedas íngremes nos valores de importância relativa de uma variável para a próxima variável podem orientar as decisões sobre quais variáveis devem ser controladas ou monitoradas. Por exemplo, nesses dados, as 2 variáveis mais importantes têm valores de importância que estão relativamente próximos antes de uma queda de mais de 20% em importância relativa para a próxima variável. Da mesma forma, 2 variáveis têm valores de importância semelhantes acima de 60%. Você pode remover variáveis de diferentes grupos e refazer a análise para avaliar como as variáveis em vários grupos afetam os valores de exatidão da predição na tabela Sumário do modelo.
Passo 3: Explore os efeitos dos preditores
Use os gráficos de dependência parcial, as funções de base e os coeficientes na equação de regressão para determinar o efeito dos preditores. Os efeitos dos preditores explicam a relação entre os preditores e a resposta. Considere todas as funções de base para um preditor entender o efeito do preditor na variável de resposta.
Além disso, considere o uso dos preditores importantes e as formas de seus relacionamentos ao construir outros modelos. Por exemplo, se o modelo de regressão MARS® incluir interações, considere se essas interações devem ser incluídas em um modelo de regressão de mínimos quadrados para comparar o desempenho dos dois tipos de modelos. Em aplicativos em que você controla os preditores, os efeitos fornecem uma maneira natural de otimizar as configurações para atingir uma meta para a variável de resposta.
Em um modelo aditivo, gráficos de dependência parcial de um preditor mostram como os importantes preditores contínuos afetam a resposta prevista. O gráfico de dependência parcial com um preditor indica como a resposta deve mudar com modificações nos níveis do preditor. Para Regressão MARS®, os valores no gráfico vêm das funções de base para o preditor no eixo x. A contribuição no eixo y é padronizada de modo que o valor mínimo no gráfico seja 0.
Principal resultado: Gráfico de dependência parcial
Este gráfico ilustra que aumenta à medida que Preço de venda aumenta Área de convivência da metragem quadrada mínima no conjunto de dados para cerca de 3.000 pés quadrados. Depois de Área de convivência atingir 3.000 pés quadrados, a contribuição para se torna plana Preço de venda em aproximadamente US $ 152.000.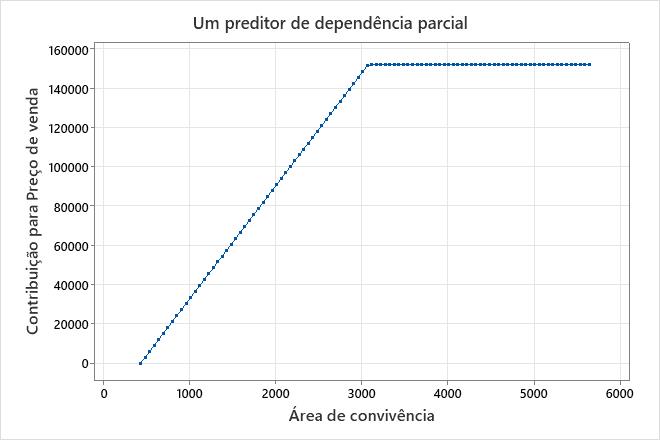
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Principal resultado: Equação de Regressão
Nesses resultados, o BF2 apresenta coeficiente negativo na equação de regressão. O coeficiente para a função base é −57,6167. O arranjo da função base é max(0, c − X). Nesse arranjo, o valor da função base diminui quando o preditor aumenta. A combinação desse arranjo com o coeficiente negativo cria uma relação positiva entre a variável preditora e a variável resposta. A inclinação de é de 57,6167 de Área de convivência 438 para 3.078.
Para obter mais exemplos de funções de base comum, vá para Equação de regressão para Regressão MARS®.
