Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
y = b0 + b1BF1 + b2BF2+ ... + bkBFk
- y é a variável resposta
- b0 é o termo constante
- b1 + b2 + ... + bk são coeficientes para as funções de base
- BF1 + BF2 + ... + BFk são as funções de base
Resolva as funções de base para valores do preditor para calcular o valor previsto da resposta.
Funções de base
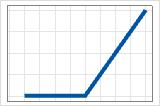
- máx(0, X − c)
- Coeficiente positivo
- A contribuição é de 0 até c, depois aumenta.
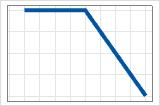
- máx(0, X − c)
- Coeficiente negativo
- A contribuição é a máxima até c, então diminui.
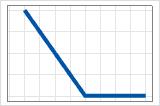
- máx(0, c − X)
- Coeficiente positivo
- A contribuição começa no máximo e diminui até c. Depois de c, a contribuição é 0.
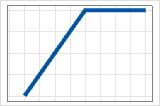
- máx(0, c − X)
- Coeficiente negativo
- A contribuição começa em 0 e aumenta até c. Depois de c, as contribuições estão no valor máximo.
Se c é igual ao valor mínimo ou máximo do preditor, então o preditor tem o mesmo efeito para todos os valores da função base. O gráfico de dependência parcial para esses 2 casos mostra uma linha reta. Regressão MARS® faz de c um dos pontos de extremidade em uma análise que não permite transformações para o preditor.
Para preditores categóricos, as funções de base são funções indicadoras. A função tem um valor de 0 para algumas categorias e um valor de 1 para as outras categorias. As funções de base têm a seguinte forma:
Quando X é x1, ... xk onde k é o número de níveis na função base,k ≥ 1.
O valor da função é 1 para as categorias na função base. A multiplicação da função base pelo coeficiente na equação de regressão determina o efeito quando a função muda de 0 para 1.
Exemplo de um preditor contínuo em 1 função de base
Nesses resultados, o BF2 apresenta coeficiente negativo na equação de regressão. O coeficiente para a função base é −57,6167. O arranjo da função base é max(0, c − X). Nesse arranjo, o valor da função base diminui quando o preditor aumenta. A combinação desse arranjo com o coeficiente negativo cria uma relação positiva entre a variável preditora e a variável resposta. O efeito disso Área de convivência é aumentar Preço de venda na região de 438 para 3.078. A inclinação de é de 57,6167 de Área de convivência 438 para 3.078.
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
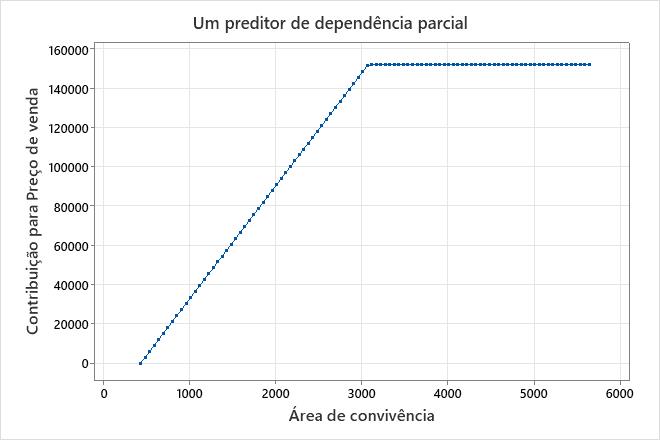
Um gráfico de dependência parcial do preditor
Em um modelo aditivo, use os gráficos de dependência parcial de um preditor para obter informações sobre como os importantes preditores contínuos afetam a resposta prevista. O gráfico de dependência parcial com um preditor indica como a resposta deve mudar com modificações nos níveis do preditor. Para Regressão MARS®, os valores no gráfico vêm das funções de base para o preditor no eixo x. A contribuição no eixo y é padronizada de modo que o valor mínimo no gráfico seja 0.
Este gráfico ilustra que aumenta à medida que Preço de venda aumenta Área de convivência da metragem quadrada mínima no conjunto de dados para cerca de 3.000 pés quadrados. Depois de Área de convivência atingir 3.000 pés quadrados, a contribuição para se torna plana Preço de venda em aproximadamente US $ 152.000.
Exemplo de um preditor categórico em 1 função de base
Nesses resultados, o BF3 é para o preditor qualidade. A função base é para quando o valor de qualidade é 8, 9 ou 10. O coeficiente para BF3 na equação é de 115.438. Essa função de base indica que, quando o valor da qualidade muda de um valor de 1 a 7 para um valor de 8, 9 ou 10, o preço de venda aumenta em US$ 115.438 no modelo. qualidade também está em BF11 e BF25. Para entender o efeito do preditor na variável resposta, considere todas as funções de base.
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Observação
Em uma equação de regressão tradicional, o coeficiente na equação de regressão sempre representa a mudança de 0 para 1. Em Regressão MARS®, o coeficiente pode representar a variação de 1 para 0. Considere uma variável categórica binária que é 0 quando um paciente relata que não tem dor de cabeça e 1 quando um paciente relata que tem dor de cabeça. Suponha que o preditor tenha a seguinte função de base:
- BF1 = quando a cefaleia é 0
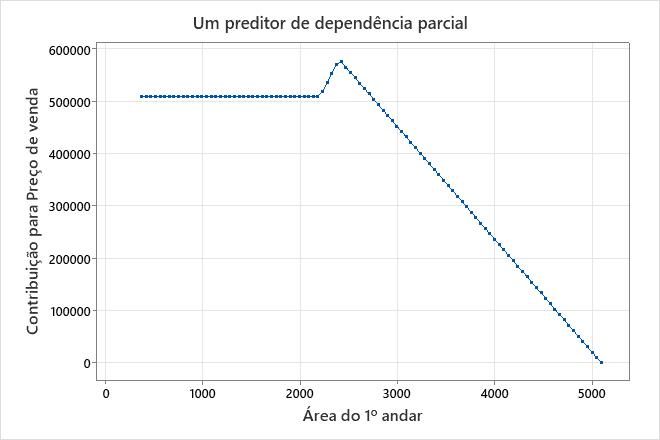
Múltiplas funções de base para 1 preditor
Regressão MARS® usa várias funções de base para um único preditor para modelar relações não lineares mais complexas entre um preditor e a resposta. Funções de base adicionais criam mudanças adicionais na inclinação da relação entre o preditor e a variável de resposta. Regressão MARS® permite preditores em múltiplas funções de base em modelos aditivos.
Nesses resultados, o BF21 é para o preditor Área do 1º andar. A função base BF27 também é para Área do 1º andar. BF21 e BF27 têm o mesmo arranjo, max(0, X − c). As funções de base neste arranjo afetam a variável de resposta quando o preditor tem um valor maior que c. Para 2 funções de base com este arranjo, nenhuma função de base afeta a resposta até que o preditor atinja o valor mínimo em 1 das funções de base. Nesses resultados, esse valor é de 2.207 no BF27. Área do 1º andar tem uma inclinação de 0 do valor mínimo até 2.207. Após 2.207, aplica-se a inclinação do BF27, o que resulta em uma inclinação de 361.254. Essa inclinação persiste até que o preditor atinja a constante no BF21, momento em que os coeficientes do BF27 e do BF21 afetam Preço de venda. A soma dos dois coeficientes dá a nova inclinação, 361,254 + (−576,789) = −215,535. Em um modelo aditivo, Regressão MARS® exibe um gráfico de dependência parcial de um preditor para mostrar o efeito do preditor.
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Funções de base para valores ausentes
Na busca pelas funções de base, Regressão MARS® cria variáveis indicadoras para quaisquer preditores com valores ausentes. A variável indicadora mostra se um valor do preditor está ausente. Se a análise incluir uma função de base para um preditor com valores ausentes no modelo, o modelo também incluirá uma função de base para a variável indicadora. As outras funções de base para o preditor interagem com a função base para a variável indicadora.
Quando um preditor tem um valor ausente, a função base para a variável indicadora anula as outras funções base para esse preditor através da multiplicação por 0. Essas funções de base para valores ausentes estão em todos os modelos em que preditores importantes têm valores ausentes, mesmo modelos aditivos e modelos que desabilitam outros tipos de transformações.
Nesses resultados, o BF7 é para o preditor Área do porão 1. O AM 7 tem um valor de 1 quando Área do porão 1 está nos dados. BF 7 tem um valor de 0 quando Área do porão 1 está faltando. O BF7 não está presente na equação de regressão porque a função base não foi importante no modelo final, mas o BF7 interage com o BF10. O BF10 é importante e está presente na equação de regressão. O efeito do BF7 é multiplicar o BF10 por 0 quando está faltando, o que remove o efeito quando Área do porão 1Área do porão 1 está faltando.
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Funções de base para interações
Para modelar interações, Regressão MARS® multiplica funções de base para diferentes preditores. Regressão MARS® O não considera as interações no modelo aditivo padrão. Gráficos de dependência parcial não estão disponíveis para uma análise que considere interações.
Uma interação significa que o efeito de um preditor depende do valor de outros preditores. Por exemplo, a taxa na qual o grão seca em um forno depende do tempo no forno, mas o efeito do tempo depende da temperatura do forno. As variáveis de tempo e temperatura interagem.
Nos resultados para um modelo com interações, BF9 é para o preditor qualidade. BF12 é para o preditor Área do 1º andar. O cálculo do BF12 inclui a multiplicação pelo BF9, de modo que os dois preditores interagem. Determinação do efeito de qualidade ou Área do 1º andar requer conhecimento do valor do outro preditor. O coeficiente para BF12 de −63,1685 aplica-se somente quando o valor de BF9 é 1. O valor de BF9 é 1 quando qualidade é 8, 9 ou 10. Devido ao arranjo de BF12, Área do 1º andar tem uma inclinação de 63,1685 quando a metragem quadrada é inferior a 2.470 e o valor de qualidade é 8, 9 ou 10.
Equação de Regressão
BF4 = máx(0, 2002 - ano construído)
BF5 = quando Área do porão 1 não está faltando
BF7 = máx(0, Área do porão 1 - 1758) * BF5
BF8 = máx(0, 1758 - Área do porão 1) * BF5
BF9 = quando qualidade é 8; 9; 10
BF12 = máx(0, 2470 - Área do 1º andar) * BF9
BF14 = quando qualidade é 7; 9; 10
BF15 = quando tipo é 75; 90; 150; 160; 180; 190
BF19 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Northridge; Northridge
Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker; Verdes * BF5
BF21 = quando Condição é 1; 2; 3; 4; 5; 6 * BF4
BF25 = máx(0, Área do 1º andar - 372) * BF7
BF26 = quando área total do porão não está faltando * BF14
BF28 = máx(0, área total do porão - 689) * BF26
Preço de venda = 320349 - 66,4387 * BF2 - 28,2065 * BF8 + 123645 * BF9 - 63,1685 * BF12 -
23751,7 * BF15 + 22818,2 * BF19 - 523,924 * BF21 - 0,036887 * BF25 + 53,9878 * BF28
