Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Uma equipe de pesquisadores coleta dados da venda de propriedades residenciais individuais em Ames, Iowa. Os pesquisadores querem identificar as variáveis que afetam o preço de venda. As variáveis incluem o tamanho do lote e várias características do imóvel residencial. Os pesquisadores querem avaliar o quão bem o melhor modelo MARS® se encaixa nos dados.
- Abra os dados amostrais, Habitação_Ames.MWX.
- Selecione .
- Em Resposta, insira “Preço de venda”.
- Em Preditores contínuos, digite ‘frontage lot' – 'ano vendido’.
- Em Preditores categóricos, digite tipo – ‘Condição de venda’.
- Clique em OK.
Interprete os resultados
Por padrão, Regressão MARS® ajusta um modelo aditivo para que todas as funções de base na equação de regressão usem 1 preditor. O primeiro preditor da lista é o BF2. BF2 usa o preditor Área de convivência. Como o preditor está em 1 função base, o preditor tem 2 inclinações diferentes no modelo. A função max(0, 3078 - Área de convivência) define que a inclinação é diferente de zero quando a área de estar é inferior a 3.078.
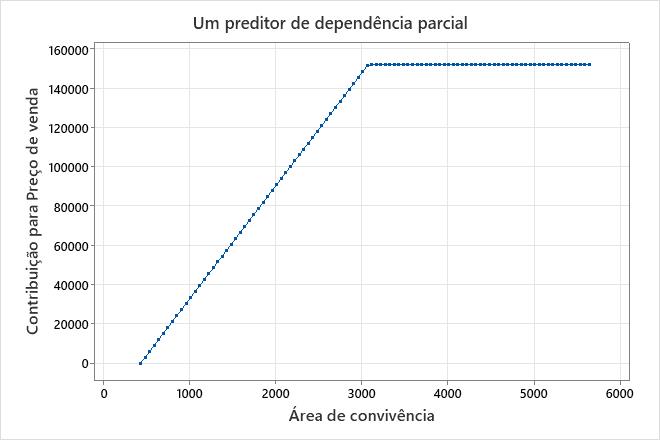
Os resultados para um modelo aditivo incluem gráficos de dependência parcial para preditores contínuos que são importantes no modelo. Use o gráfico para ver o efeito de todas as funções de base para um preditor em todo o intervalo do preditor. Nesses resultados, o gráfico de dependência parcial mostra que para um valor de 438 a 3.078, a inclinação é de cerca de Área de convivência 57,6. Quando Área de convivência for maior que 3.078, a inclinação é 0.
Nesses resultados, o BF2 apresenta coeficiente negativo na equação de regressão. O arranjo da função base é max(0, c − X). Nesse arranjo, o valor da função base diminui quando o preditor aumenta. A combinação desse arranjo com o coeficiente negativo cria uma relação positiva entre a variável preditora e a variável resposta. O efeito disso Área de convivência é aumentar Preço de venda na região de 438 para 3.078.
A análise também inclui preditores categóricos. Por exemplo, BF3 é para o preditor qualidade. A função base é para quando o valor de qualidade é 8, 9 ou 10. O coeficiente para BF3 na equação é de 115.438. Essa função de base indica que, quando o valor da qualidade muda de um valor de 1 a 7 para um valor de 8, 9 ou 10, o preço de venda aumenta em US$ 115.438 no modelo. qualidade também está em BF11 e BF25. Para entender o efeito do preditor na variável resposta, considere todas as funções de base.
Dois dos preditores que são importantes no modelo têm valores ausentes nos dados de treinamento: Área do porão 1 e área total do porão. A lista de funções de base inclui funções de base que identificam quando esses preditores estão faltando: BF7 e BF17. Quando um preditor tem um valor ausente, a função base para a variável indicadora anula as outras funções base para esse preditor através da multiplicação por 0.
Equação de Regressão
BF3 = quando qualidade é 8; 9; 10
BF6 = máx(0, 2002 - ano construído)
BF7 = quando Área do porão 1 não está faltando
BF10 = máx(0, 1696 - Área do porão 1) * BF7
BF11 = quando qualidade é 1; 8
BF13 = quando tipo é 90; 150; 160; 180; 190
BF15 = quando Bairro é Bluestem; Clear Creek; Crawford; Green Hills; Marco; Northridge;
Northridge Heights; Ponte de Pedra; Somerset Villages; Timberland; Veenker
BF17 = quando área total do porão não está faltando
BF19 = máx(0, área total do porão - 1392) * BF17
BF21 = máx(0, Área do 1º andar - 2402)
BF23 = quando Condição é 1; 2; 3; 4; 5; 6
BF25 = quando qualidade é 1; 7; 10
BF27 = máx(0, Área do 1º andar - 2207)
BF30 = máx(0, 15138 - área de lote)
Preço de venda = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Observação
Nestes resultados, a lista de funções de base tem 15 funções de base, mas o número ótimo de funções de base é 13. A equação de regressão contém 13 funções de base. A lista de funções base contém BF7 e BF17, que são as funções base que identificam os valores ausentes. Essas funções de base não são importantes por si só porque não reduziram o MSE tanto quanto outras funções de base na pesquisa. Essas 2 funções de base estão na lista para mostrar o cálculo completo do BF10 e do BF 19, que são importantes.
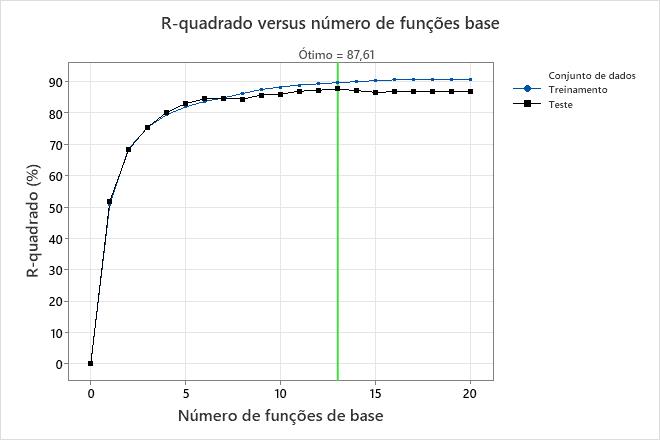
O gráfico R-quadrado vs Número de Funções de Base mostra o resultado da eliminação para trás para encontrar o número ideal de funções de base. Para usar um modelo com um número diferente de funções base, selecione Selecione o modelo alternativo. Por exemplo, se um modelo com muito menos funções de base é quase tão preciso quanto o modelo ideal, considere se deve usar o modelo mais simples. Nesses resultados, os valores de R-quadrado para os conjuntos de dados de treinamento e teste são os mesmos para o modelo com 7 funções de base. Este modelo menor é de interesse se o excesso de ajuste for uma preocupação.
Sumário do modelo
| Preditores totais | 77 |
|---|---|
| Preditores importantes | 10 |
| Número máximo de funções base | 30 |
| Número ótimo de funções base | 13 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| R-quadrado | 89,61% | 87,61% |
| Raiz do quadrado médio do Erro (RMSE) | 25836,5197 | 27855,6550 |
| Quadrado médio do erro (MSE) | 667525749,7185 | 775937512,8264 |
| Desvio absoluto médio (DAM) | 17506,0038 | 17783,5549 |
A tabela de resumo do modelo inclui medidas de quão bem o modelo executa. Você pode usar esses valores para comparar modelos. Para estes resultados, o teste R-quadrado é de cerca de 88%.
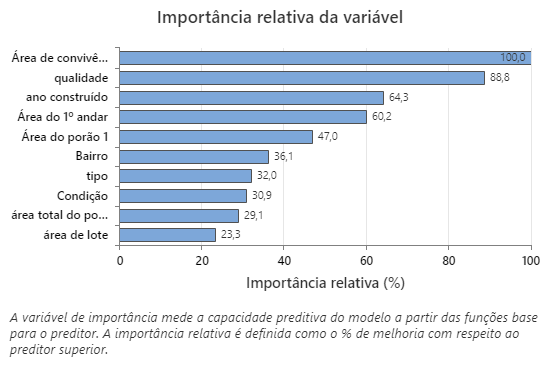
O gráfico de importância da variável relativa plota os preditores em ordem de seu efeito no modelo. A variável preditora mais importante é Área de convivência. Se a contribuição da variável preditora superior, Área de convivência, é de 100%, então a próxima variável importante, qualidade, tem uma contribuição de 44,4 %. Essa contribuição significa que qualidade é 88,8% tão importante quanto Área de convivência nesse modelo.
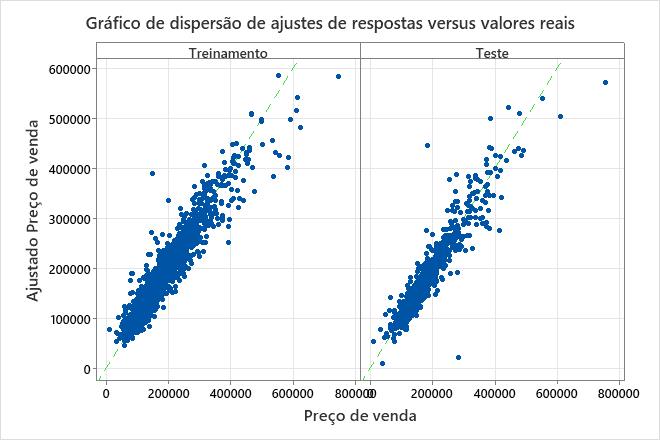
O gráfico de dispersão dos preços de venda ajustados versus os preços de venda reais mostra a relação entre os valores ajustados e os valores reais para os dados de formação e os dados de ensaio. Você pode passar o mouse sobre os pontos no gráfico para ver mais facilmente os valores representados graficamente. Neste exemplo, a maioria dos pontos cai aproximadamente perto da linha de referência de y=x.
O modelo se encaixa mal em alguns pontos distintos, como o do conjunto de dados de teste que tem um preço de venda ajustado de menos de US $ 100.000, mas um preço de venda real mais próximo de US $ 250.000. Considere se deve investigar este caso para melhorar o ajuste do modelo.
