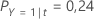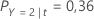Uma árvore de classificação resulta de uma partição recursiva binária do conjunto de dados de treinamento original. Qualquer nó pai (um subconjunto de dados de treinamento) em uma árvore pode ser dividido em dois nós filhos mutuamente exclusivos de um número finito de maneiras, o que depende dos valores dos dados reais coletados no nó.
O procedimento de divisão trata as variáveis preditoras como contínuas ou categóricas. Para uma variável contínua X e um valor c, uma divisão é definida enviando todos os registros com os valores de X menores ou iguais a c para o nó esquerdo, e todos os registros restantes para o nó direito. O CART sempre utiliza a média de dois valores adjacentes para calcular c. Uma variável contínua com valores N distintos gera até N-1 divisões potenciais do nó pai (o número real será menor quando houver imposição de limites sobre o tamanho mínimo permitido para o nó).
Por exemplo, um preditor contínuo tem os valores 55, 66 e 75 nos dados. Uma possível divisão para essa variável é enviar todos os valores menores ou iguais a (55+66)/2 = 60,5 para um nó filho e todos os valores superiores a 60,5 para o outro nó filho. Os casos com o valor preditor de 55 vão para um nó e os casos com os valores 66 e 75 vão para o outro nó. A outra possível divisão para este preditor é enviar todos os valores menores ou iguais a 70,5 para um nó filho e valores superiores a 70,5 para o outro nó. Os casos com os valores 55 e 66 vão para um nó, e os casos com o valor 75 vão para o outro nó.
Para uma variável categórica X com valores distintos {c1, c2, …, ck}, uma divisão é definida como um subconjunto de níveis que são enviados para o nó filho esquerdo. Uma variável categórica com K níveis gera até 2K-1– 1 divisões.
| Nó filho esquerdo | Nó filho direito |
|---|---|
| Vermelho, Azul | Amarelo |
| Vermelho, Amarelo | Azul |
| Azul, Amarelo | Vermelho |
Nas árvores de classificação, o alvo é multinomial com classes K distintas. O principal objetivo da árvore é encontrar uma maneira de separar diferentes classes-alvo em nós individuais da maneira mais pura possível. O número resultante de nós terminais não precisa ser K; vários nós terminais podem ser usados para representar uma classe-alvo específica. Um usuário pode especificar probabilidades a priori para as classes-alvo; estas serão contabilizadas pelo CART durante o processo de crescimento das árvores.
Nas próximas seções, o Minitab usa as seguintes definições para uma variável resposta binária:
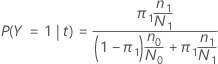
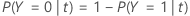
Nas próximas seções, o Minitab usa as seguintes definições para uma variável resposta multinomial:
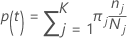
A probabilidade de classe j dado o nó t:
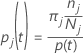
Essas definições fornecem as probabilidades de dentro do nó. O Minitab calcula essas probabilidades para qualquer nó e qualquer divisão potencial. O Minitab calcula a melhoria geral para uma divisão potencial dessas probabilidades com um dos critérios a seguir.
Notação
| Termo | Descrição |
|---|---|
| K | número de classes na variável resposta |
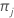 | probabilidade a priori para classe j |
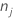 | número de observações para classe j em um nó |
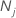 | número de observações para classe j nos dados |
Critério de Gini
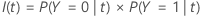
A fórmula mais geral a seguir se aplica a uma variável resposta multinomial:
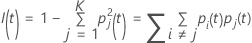
Veja que se todas as observações para um nó estão em uma única classe, então
 .
.
Critério de entropia

A fórmula mais geral a seguir se aplica a uma variável resposta multinomial:
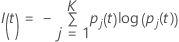
Veja que se todas as observações para um nó estão em uma única classe, então
 .
.
Critério de Twoing
| Superclasse 1 | Superclasse 2 |
|---|---|
| 1, 2, 3 | 4 |
| 1, 2, 3 | 3 |
| 1, 3, 4 | 2 |
| 2, 3, 4 | 1 |
| 1, 2 | 3, 4 |
| 1, 3 | 2, 4 |
| 1, 4 | 2, 3 |


A superclasse esquerda tem todas as classes-alvo que tendem a ir para a esquerda. A superclasse direita tem todas as classes-alvo que tendem a ir para a direita.
| Classe | Probabilidade de nó filho esquerdo | Probabilidade de nó filho direito |
|---|---|---|
| 1 | 0,67 | 0,33 |
| 2 | 0,82 | 0,18 |
| 3 | 0,23 | 0,77 |
| 4 | 0,89 | 0,11 |
Assim, a melhor maneira de formar as superclasses para a divisão de candidato é atribuir {1, 2, 4} como uma superclasse e {3} como a outra superclasse.
O resto do cálculo é igual ao do critério de Gini com as superclasses, como o alvo binário.
Cálculo de melhoria para os critérios
Depois que o Minitab calcula a impureza do nó, passa ao cálculo das probabilidades condicionais para a divisão do nó com um preditor:
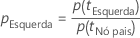
e

Em seguida, a melhoria para uma divisão é dada pela seguinte fórmula:
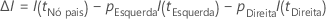
A divisão com o maior valor de melhoria torna-se parte da árvore. Se a melhoria para dois preditores for a mesma, o algoritmo requer uma seleção para prosseguir. A seleção utiliza um esquema determinístico de desempate que envolve a posição dos preditores na planilha, o tipo de preditor e o número de aulas em um preditor categórico.
Probabilidade de classe
As divisões do nó maximizam a probabilidade de uma classe dentro de um determinado nó.
Nós terminais
- O número de casos no nó atinge o tamanho mínimo para a análise. O padrão mínimo no Minitab Statistical Software é de 3.
- Todos os casos em um nó têm a mesma classe de resposta.
- Todos os casos em um nó têm os mesmos valores preditores.
Classe predita para um nó terminal
A classe predita para um nó terminal é a classe que minimiza o custo de classificação errada para o nó. As representações do custo de classificação errada dependem do número de classes na variável resposta. Como a classe predita para um nó terminal vem dos dados de treinamento quando você usa um método de validação, todas as fórmulas a seguir usam probabilidades do conjunto de dados de treinamento.
Variável resposta binária
A equação a seguir fornece ao custo de classificação errada para a predição de que os casos no nó sejam a classe de evento:

A equação a seguir fornece ao custo de classificação errada para a predição de que o caso no nó seja a classe de não evento:

| Termo | Descrição |
|---|---|
| PY=0|t | probabilidade condicional de que um caso no nó t pertence à classe de não evento |
| C1|0 | custo de classificação errada que um caso de classe de não evento é predito como um caso de classe de evento |
| PY=1|t | probabilidade condicional de que um caso no nó t pertence à classe de evento |
| C0|1 | custo de classificação errada que um caso de classe de evento é predito como um caso de classe de não evento |
A classe predita para um nó terminal é a classe com o custo mínimo de classificação errada.
Variável resposta multinomial

Por exemplo, considere uma variável resposta com três classes e os seguintes custos de classificação errada:
| Classe predita | |||
| Classe real | 1 | 2 | 3 |
| 1 | 0,0 | 4,1 | 3,2 |
| 2 | 5,6 | 0,0 | 1,1 |
| 3 | 0,4 | 0,9 | 0,0 |
Então, considere que as classes da variável resposta têm as seguintes probabilidades para o nó t:
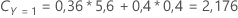


O menor custo de classificação é para a predição de que Y = 3, 1,164. Esta classe é a classe predita para o nó terminal.