Métodos e fórmulas para o sumário do modelo em Classificação CART^®

Selecione o método ou fórmula de sua preferência.

Neste tópico

Preditores importantes
Média − Log-verossimilhança
Área sob a curva ROC

IC de 95% para a área sob a curva ROC
Ganho
Custo de classificação errada

Preditores importantes

O número de preditores com importância relativa positiva.

Qualquer árvore de classificação é uma coleção de divisões. Cada divisão proporciona melhorias à árvore. Cada divisão também inclui divisões de substitutos que também proporcionam melhorias na árvore. A importância de uma variável é dada por todas as suas melhorias quando a árvore usa a variável para dividir um nó ou como substituto para dividir um nó quando outra variável tem um valor faltante.

A fórmula a seguir fornece a melhoria em um único nó:

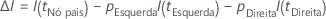
Os valores de I(t),p_Esquerda, e p_Direita dependem do critério para dividir os nós. Para obter mais informações, acesse Métodos de divisão de nós em Classificação CART®.

A fórmula para a importância relativa do q^o preditor dimensiona a importância pela variável mais importante:

Média − Log-verossimilhança

O Minitab calcula a média da função de log-verossimilhança negativa quando a resposta é binária. Os cálculos dependem do método de validação.

Dados de treinamento ou sem validação

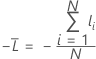
em que

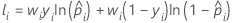
Notação para dados de treinamento ou sem validação

Termo	Descrição
N	tamanho amostral dos dados completos ou dos dados de treinamento
w_i	peso para a i^a observação no conjunto de dados completo ou de treinamento
y_i	variável indicadora que é 1 para o evento e 0 em outros casos para o conjunto completo ou de dados de treinamento
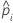	probabilidade predita do evento para a i^a linha no conjunto de dados completo ou de treinamento

Validação cruzada de K dobras

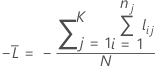
em que

Notação para validação cruzada de K dobras

Termo	Descrição
N	tamanho amostral dos dados completos ou de treinamento
n_j	tamanho amostral da dobra j
w_ij	peso para a i^a observação na dobra j
y_ij	variável indicadora que é 1 para evento e 0 em outros casos para os dados na dobra j
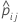	probabilidade predita do evento a partir da estimativa do modelo que não inclui as observações para a i^a observação na dobra j

Conjunto de dados de teste

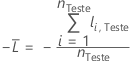
em que

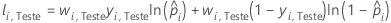
Notação para o conjunto de dados de teste

Termo	Descrição
n_teste	tamanho amostral do conjunto de teste
w_i_{, teste}	peso para a i^a observação no conjunto de dados de teste
y_i_{, teste}	variável indicadora que é 1 para evento e 0 em outros casos para os dados no conjunto de teste
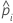	probabilidade predita do evento para a i^a linha no conjunto de teste

Área sob a curva ROC

A curva ROC traça a taxa de positivos verdadeiros (TPR), também conhecida como poder, no eixo Y, e a taxa de falsos positivos (FPR), também conhecida como erro tipo 1, no eixo x. A área sob os valores da curva ROC variam tipicamente de 0,5 a 1.

Fórmula

Para a área sob a curva, o Minitab utiliza uma integração.

Na maioria dos casos, essa integral equivale à soma das seguintes áreas de trapezoides:

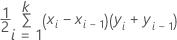
em que k é o número de nós terminais e (x₀, y₀) é o ponto (0, 0).

Por exemplo, suponha que seus resultados tenham 4 nós terminais com as seguintes coordenadas na curva ROC:

x (taxa de falsos positivos)	y (taxa de positivos verdadeiros)
0,0923	0,3051
0,4154	0,7288
0,7538	0,9322
1	1

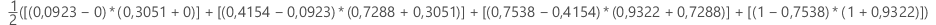
Em seguida, a área sob a curva ROC é dada pelo seguinte cálculo:

Notação

Termo	Descrição
TRP	taxa de positivos verdadeiros
FPR	taxa de falsos positivos
TP	positivos verdadeiros, eventos que foram corretamente avaliados
P	número de eventos positivos reais
FP	negativos verdadeiros, não eventos que foram corretamente avaliados
N	número de eventos negativos reais
FNR	taxa de falsos negativos
TNR	taxa de negativos verdadeiros

IC de 95% para a área sob a curva ROC

O Minitab calcula um intervalo de confiança para a área sob a curva característica de operação do receptor quando a resposta é binária.

O intervalo a seguir fornece os limites superiores e inferiores para o intervalo de confiança:

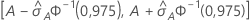
O cálculo do erro padrão da área sob a curva ROC (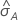) vem de Salford Predictive Modeler^®. Para obter informações gerais sobre a estimativa da variância da área sob a curva ROC, consulte as seguintes referências:

Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2ª ed.) Heidelberg; Nova York: Springer. doi:10.1007/978-3-642-16114-8

Cortes, C. e Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.

Feng, D., Cortese, G., e Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040

Notação

Termo	Descrição
A	área sob a curva ROC
	0,975 percentil da distribuição normal padrão

Ganho

O Minitab exibe o ganho na tabela de sumária do modelo quando a resposta é binária. A elevação na tabela do sumário do modelo é o ganho acumulado para os 10% dos dados com a melhor chance de classificação correta.

Fórmula

Para os 10% das observações nos dados com as probabilidades mais altas serem atribuídos à classe de eventos, use a seguinte fórmula.

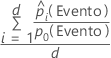
Para o ganho de teste com um conjunto de dados de teste, use as observações do conjunto de dados de teste. Para o ganho do teste com validação cruzada em de K dobras, selecione os dados a serem usados e calcule o ganho das probabilidades preditas para dados que não estão na estimativa do modelo.

Notação

Termo	Descrição
d	número de casos em 10% dos dados
	probabilidade predita do evento
	probabilidade de evento nos dados de treinamento ou, se a análise não utilizar validação, no conjunto de dados completo

Custo de classificação errada

O custo de classificação errada na tabela de sumário do modelo é o custo relativo de classificação errada para o modelo em relação a um classificador trivial que classifica todas as observações na classe mais frequente.

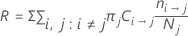
Para encontrar o custo de classificação errada, comece com a seguinte definição:

O custo relativo de classificação errada tem a seguinte forma:

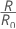
Em que R₀ ié o custo para o classificador trivial.

A fórmula para R simplifica quando as probabilidades a priori são iguais ou são provenientes dos dados.

Probabilidades a priori iguais

Quando as probabilidades a priori são iguais, aplica-se a seguinte definição:

Com esta definição, R tem a seguinte forma:

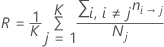
Probabilidades a priori dos dados

Quando as probabilidades a priori são provenientes dos dados, aplica-se a seguinte definição:

Com esta definição, R tem a seguinte forma:

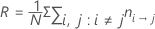
Notação

Termo	Descrição
π_j	probabilidade a priori da j^a classe da variável resposta
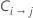	custo de classificar errado a classe i como classe j
	Número de registros da classe i classificados incorretamente como classe j
N_j	número de casos na j^a classe da variável resposta
K	número de classes na variável resposta
N	número de casos nos dados

Métodos e fórmulas para o sumário do modelo em Classificação CART®

Neste tópico

Preditores importantes

Média − Log-verossimilhança

Dados de treinamento ou sem validação

Notação para dados de treinamento ou sem validação

Validação cruzada de K dobras

Notação para validação cruzada de K dobras

Conjunto de dados de teste

Notação para o conjunto de dados de teste

Área sob a curva ROC

Fórmula

Notação

IC de 95% para a área sob a curva ROC

Notação

Ganho

Fórmula

Notação

Custo de classificação errada

Probabilidades a priori iguais

Probabilidades a priori dos dados

Notação

Métodos e fórmulas para o sumário do modelo em Classificação CART^®