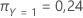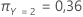Métodos e fórmulas para a classificação errada em Classificação CART^®

Selecione o método ou fórmula de sua preferência.

Neste tópico

Contagem
Contagem ponderada
% de erro
Custo

A tabela de classificação errada não está presente quando o método de divisão é a probabilidade de classe.

Contagem

Quando não há pesos, as contagens e os tamanhos das amostras são os mesmos.

Contagem ponderada

No caso ponderado, a contagem ponderada é a soma dos pesos para uma categoria. As contagens ponderadas são arredondadas para o número inteiro mais próximo. Use os pesos não arredondados para calcular percentagens e taxas. Considere o seguinte exemplo simples:

Nível de resposta	Nível predito	Peso
Sim	Sim	0,1
Sim	Sim	0,2
Sim	Não	0,3
Sim	Não	0,4
Não	Não	0,5
Não	Não	0,6
Não	Sim	0,7
Não	Sim	0,8

Esta tabela fornece as seguintes estatísticas:

Classe real	Contagem ponderada	Classificado incorretamente	Classe predita = Não	Por cento correto
Sim	0,1 + 0,2 + 0,3 + 0,4 = 1	0,1 + 0,2 = 0,3 ≈ 0	0,3 + 0,4 = 0,7 ≈ 1	(0,3 / 1,0) ×100 = 30%
Não	0,5 + 0,6 + 0,7 + 0,8 = 2,6 ≈ 3	0,7 + 0,8 = 1,5 ≈ 2	0,5 + 0,6 = 1,1 ≈ 1	1,1 / 2,6) × 100 = 42,31%
Todas	1 + 2,6 = 3,6 ≈ 4	0,3 + 1,5 = 1,8 ≈ 2	0,7 + 1,1 = 1,8 ≈ 2	(0,3 + 1,1) / 3,6 × 100 = 38,89%

% de erro

No caso ponderado, use a contagem ponderada em vez da contagem.

Custo

O cálculo do custo dependerá de a variável resposta ser binária ou multinomial.

Custo = (% de erro × Custo de classificação errada de entrada para a classe) / 100

Variável resposta binária

A equação a seguir fornece o custo para a classe de evento:

A equação a seguir fornece o custo para a classe de não evento:

A equação a seguir fornece o custo total para todas as classes:

Variável resposta multinomial

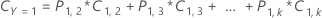
Para o caso multinomial, a equação estende a fórmula para que a variável resposta binária responda por todos os tipos possíveis de classificações erradas. Por exemplo, para uma resposta multinomial com k classes, o custo de classificação errada para Y = 1 usa a seguinte equação:

A equação a seguir fornece o custo total para o caso multinomial:

Por exemplo, considere uma variável resposta com 3 classes e os seguintes custos de classificação errada:

	Classe predita
Classe real	1	2	3
1	0,0	4,1	3,2
2	5,6	0,0	1,1
3	0,4	0,9	0,0

Então, considere que a tabela a seguir fornece as porcentagens de erro:

	Classe predita
Classe real	1	2	3
1	N/D	1%	0,5%
2	1,4%	N/D	2,1%
3	5%	1,2%	N/D

Por fim, considere que as classes da variável resposta têm as seguintes probabilidades a priori:

As equações a seguir fornecem os custos associados à classificação errada para cada classe na variável resposta:

A equação a seguir fornece o custo total:

Métodos e fórmulas para a classificação errada em Classificação CART®