Neste tópico
Passo 1: Investigue as árvores alternativas
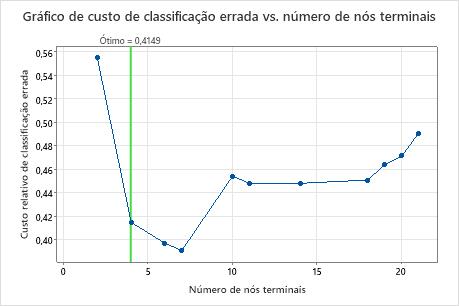
O gráfico de Custo de classificação errada vs Número de nós terminais mostra o custo de classificação errada de cada árvore na sequência que produz a árvore ótima. Por padrão, a árvore ótima inicial é a menor árvore com um custo de classificação errada dentro de um erro padrão da árvore que minimiza o custo de classificação errada. Quando a análise utiliza validação cruzada ou um conjunto de dados de teste, o custo de classificação errada vem da amostra de validação. Os custos de classificação errada para a amostra de validação normalmente nivelam e eventualmente aumentam à medida que a árvore cresce.
- A árvore ótima é parte de um padrão quando os custos de classificação errada diminuem. Uma ou mais árvores que têm mais alguns nós fazem parte do mesmo padrão. Normalmente, é aconselhável fazer predições de uma árvore com o máximo de exatidão de predição possível. Se a árvore é simples o suficiente, também é possível usá-la para entender como cada variável preditora afeta os valores de resposta.
- A árvore ótima é parte de um padrão quando os custos de classificação errada são relativamente constantes. Uma ou mais árvores com estatística semelhantes de sumário do modelo têm muito menos nós do que a árvore ótima. Normalmente, uma árvore com menos nós terminais proporciona uma visão mais clara de como cada variável preditora afeta os valores de resposta. Uma árvore menor também facilita a identificação de alguns grupos-alvo para a realização de estudos adicionais. Se a diferença na exatidão da predição para uma árvore menor for insignificante, você também pode usar a árvore menor para avaliar as relações entre a resposta e as variáveis preditoras.
Sumário do modelo
| Preditores totais | 13 |
|---|---|
| Preditores importantes | 13 |
| Número de nós terminais | 4 |
| Tamanho mínimo do nó terminal | 27 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| -Log da Verossimilhança Média | 0,4772 | 0,5164 |
| Área sob a curva ROC | 0,8192 | 0,8001 |
| IC de 95% | (0,3438; 1) | (0,7482; 0,8520) |
| Elevação | 1,6189 | 1,8849 |
| Custo de classificação errada | 0,3856 | 0,4149 |
Principais resultados: Gráfico e sumário do modelo para árvore com 4 nós
A árvore na sequência com 4 nós tem um custo de classificação errada próximo a 0,41. O padrão quando o custo de classificação errada diminui continua após a árvore de 4 nós. Em um caso como este, os analistas optam por explorar algumas das outras árvores simples que têm menores custos de classificação errada.
Sumário do modelo
| Preditores totais | 13 |
|---|---|
| Preditores importantes | 13 |
| Número de nós terminais | 7 |
| Tamanho mínimo do nó terminal | 5 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| -Log da Verossimilhança Média | 0,3971 | 0,5094 |
| Área sob a curva ROC | 0,8861 | 0,8200 |
| IC de 95% | (0,5590; 1) | (0,7702; 0,8697) |
| Elevação | 1,9376 | 1,8165 |
| Custo de classificação errada | 0,2924 | 0,3909 |
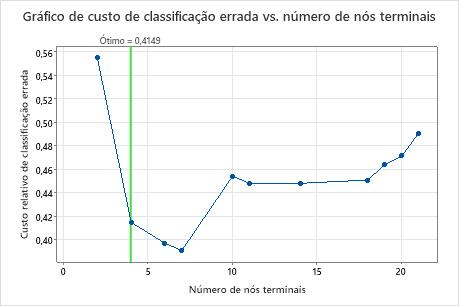
Principais resultados: Gráfico e sumário do modelo para árvore com 7 nós
A árvore de classificação que minimiza o custo relativo de classificação errada com validação cruzada tem 7 nós terminais e um custo relativo de classificação errada de aproximadamente 0,39. Outras estatísticas, como a área sob a curva ROC também confirmam que a árvore de 7 nós apresenta um desempenho melhor que a árvore de 4 nós. Como a árvore de 7 nós tem poucos nós suficientes que também é fácil de interpretar, os analistas decidem usar a árvore de 7 nós para estudar as variáveis importantes e fazer predições.
Passo 2: Investigue os nós terminais mais puros no diagrama de árvore
Depois de selecionar uma árvore, investigue os nós terminais mais puros no diagrama. Azul representa o nível do evento, e a Vermelho representa o nível não evento.
Observação
Você pode clicar com o botão direito do mouse sobre o diagrama de árvore para mostrar a visualização da divisão do nó da árvore. Essa visualização é útil quando você tem uma árvore grande e quer ver apenas as variáveis que dividem os nós.
Os nós continuam a ser divididos até que os nós terminais não possam mais ser divididos em agrupamentos adicionais. Os nós que são majoritariamente azuis indicam uma forte proporção do nível de evento. Os nós que são majoritariamente vermelhos indicam uma forte proporção do nível de não evento.
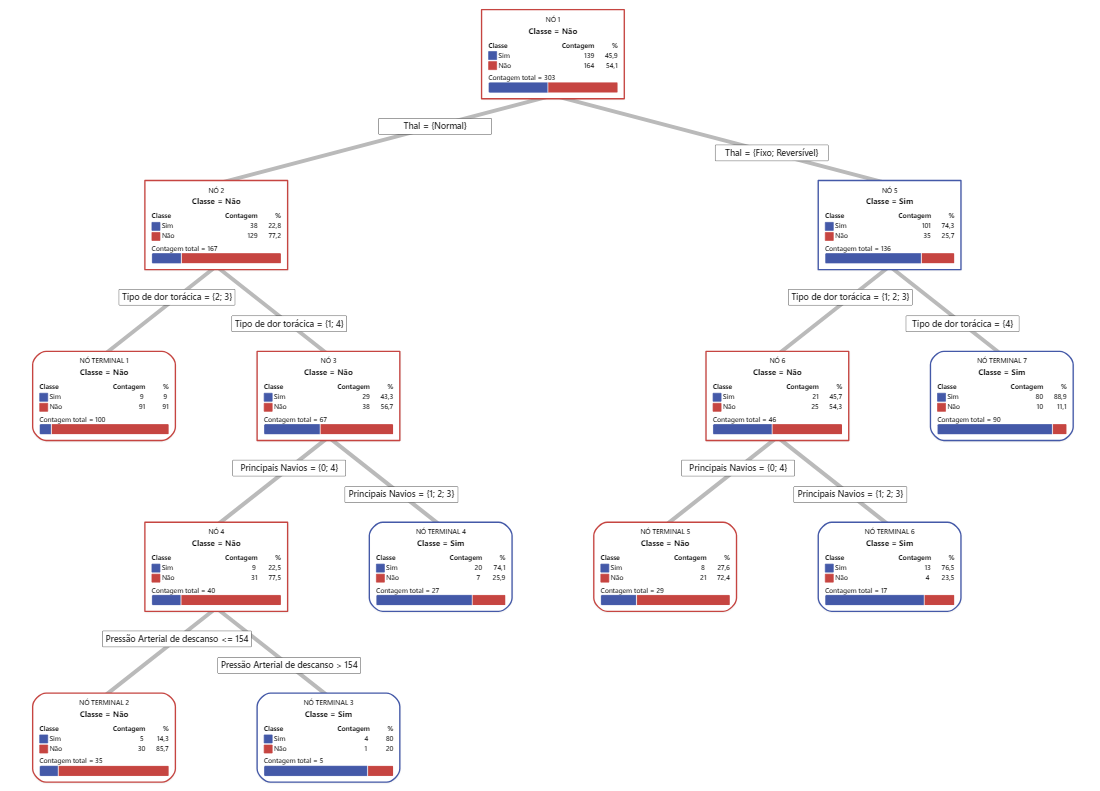
Principal resultado: Diagrama de árvore
Esta árvore de classificação tem 7 nós terminais. Azul é para o nível de evento (Sim) e Vermelho é para o nível de não evento (Não). O diagrama de árvore usa o conjunto de dados de treinamento. Você pode alternar as visualizações da árvore entre a vista detalhada e dividida do nó.
- Nó 2: O THAL era Normal para 167 casos. Dos 167 casos, 38 ou 22,8% são Sim e 129 ou 77,2% são Não.
- Nó 5: O THAL era Fixo ou Reversível para 136 casos. Dos 136 casos, 101 ou 74,3% são Sim e 35 ou 25,7% são Não.
O próximo divisor para o nó filho esquerdo e o nó filho direito é o Tipo dor no peito, em que a dor é classificada como 1, 2, 3 ou 4. O Nó 2 é o pai do Nó Terminal 1, e o Nó 5 é o pai do Nó Terminal 7.
- Nó Terminal 1: Para 100 casos, o THAL era Normal, e Dor torácica era 2 ou 3. Dos 100 casos, 9 ou 9% são Sim e 91 ou 91% são Não.
- Nó Terminal 7: Para 90 casos, o THAL era Fixo ou Reversível, e Dor torácica era 4. Dos 90 casos, 80 ou 88,9% são Sim e 10 ou 11,1% são Não.
Passo 3: Determine as variáveis importantes
Use o gráfico de importância relativa da variável para determinar quais preditores são as variáveis mais importantes para a árvore.
As variáveis importantes são um divisor primário ou substituto na árvore. A variável com maior pontuação de melhoria é definida como a variável mais importante, e as outras variáveis são classificadas de acordo. A importância relativa da variável padroniza os valores de importância para facilitar a interpretação. A importância relativa é definida como a melhoria percentual em relação ao preditor mais importante.
Os valores da importância relativa da variável variam de 0% a 100%. A variável mais importante sempre tem uma importância relativa de 100%. Se uma variável não estiver na árvore, essa variável não é importante.
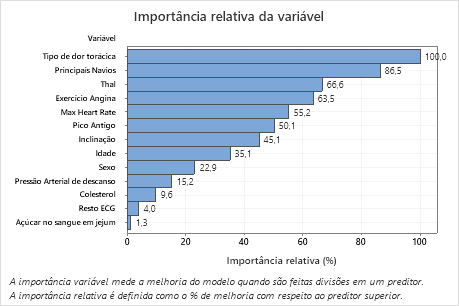
Principal resultado: Importância relativa da variável
- Principais Navios é cerca de 87% tão importante quanto Tipo de dor torácica.
- Thal e Exercício Angina ambos são cerca de 65% tão importantes quanto Tipo de dor torácica.
- Max Heart Rate é cerca de 55% tão importante quanto Tipo de dor torácica.
- Pico Antigo é cerca de 50% tão importante quanto Tipo de dor torácica.
- Inclinação, Idade, Sexo, e Pressão Arterial de descanso são muito menos importantes que Tipo de dor torácica.
Embora tenham importância positiva, os analistas podem decidir que Colesterol, Resto ECG, e Açúcar no sangue em jejum não são contribuintes importantes para a árvore.
Passo 4: Avalie o poder preditivo de sua árvore
A árvore mais exata é aquela com o menor custo de classificação errada. Às vezes, árvores mais simples com custos mais altos de classificação errada funcionam igualmente bem. Você pode usar o gráfico de custo de classificação incorreta versus nós terminais para identificar árvores alternativas.
A curva característica de operação do receptor (ROC) mostra o se uma árvore classifica bem os dados. A curva ROC traça a taxa de positivos verdadeiros no eixo Y e a taxa de falsos positivos no eixo X. A taxa de positivos verdadeiros também é conhecida como poder. A taxa de falsos positivos também é conhecida como erro tipo I.
Quando uma árvore de classificação consegue separar perfeitamente as categorias na variável resposta, então a área sob a curva ROC é 1, que é o melhor modelo de classificação possível. Em contrapartida, se uma árvore de classificação não consegue distinguir as categorias e faz atribuições de maneira completamente aleatória, a área sob a curva ROC é 0,5.
Quando você usa uma técnica de validação para construir a árvore, o Minitab fornece informações sobre o desempenho da árvore nos dados de treinamento e de validação (teste). Quando as curvas estão próximas, você pode ter maior confiança de que a árvore não está superajustada. O desempenho da árvore com os dados do teste indica se a árvore apresenta boa predição de novos dados.
- Taxa de positivos verdadeiros (TPR) — a probabilidade da ocorrência de um evento seja predita corretamente
- Taxa de falsos positivos (FPR) — a probabilidade de que a ocorrência de um não evento seja predita incorretamente
- Taxa falsos negativos (FNR) — a probabilidade de que a ocorrência de um evento seja predita incorretamente
- Taxa de negativos verdadeiros (TNR) — a probabilidade de que a ocorrência de não evento seja predita corretamente
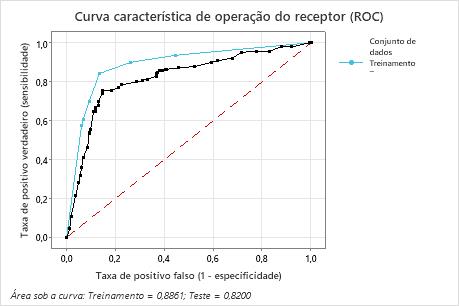
Principal resultado: Curva característica de operação do receptor (ROC)
Por este exemplo, a área sob a curva ROC é 0,886 para Treinamento e 0,82 para Teste. Esses valores indicam que, na maioria das aplicações, a árvore de classificação é um classificador razoável.
Matriz de confusão
| Classe predita (Treinamento) | |||||||
|---|---|---|---|---|---|---|---|
| Classe predita (Teste) | |||||||
| Classe real | Contagem | Sim | Não | % Correto | Sim | Não | % Correto |
| Sim (Evento) | 139 | 117 | 22 | 84,2 | 105 | 34 | 75,5 |
| Não | 164 | 22 | 142 | 86,6 | 24 | 140 | 85,4 |
| Todos | 303 | 139 | 164 | 85,5 | 129 | 174 | 80,9 |
| Estatísticas | Treinamento (%) | Teste (%) |
|---|---|---|
| Taxa de positivo verdadeiro (sensibil. ou poder) | 84,2 | 75,5 |
| Taxa de positivo falso (erro tipo I) | 13,4 | 14,6 |
| Taxa de negativo falso (erro tipo II) | 15,8 | 24,5 |
| Taxa de negativo verdadeiro (especificidade) | 86,6 | 85,4 |
Principal resultado: Matriz de confusão
- Taxa de positivos verdadeiros (TPR) — 84,2% para os dados de treinamento e 75,5% para os dados de teste
- Taxa de falsos positivos (FPR) — 13,4% para os dados de treinamento e 14,6% para os dados de teste
- Taxa de falsos negativos (FNR) — 15,8% para os dados de treinamento e 24,5% para os dados do teste
- Taxa de negativos verdadeiros (TNR) — 86,6% para os dados de treinamento e 85,4% para os dados de teste
No geral, o %Corretos para os dados de treinamento é de 85,5% e para os dados do teste é de 80,9%.
