Uma probabilidade posterior é a probabilidade de atribuir observações a grupos considerando-se os dados. Uma probabilidade anterior é a probabilidade de que uma observações estará em um grupo antes de se coletar os dados. Por exemplo, se você está classificando os compradores de um carro específico, você poderia saber de antemão que 60% dos compradores são homens e 40% são mulheres. Se você conhece ou pode estimar essas probabilidades, uma análise discriminante pode usar essas probabilidades anteriores para calcular as probabilidades posteriores. Quando você não especifica probabilidades anteriores, o Minitab pressupõe que os grupos são igualmente prováveis.
Com a pressuposição de que os dados possuem uma distribuição normal, a função discriminante linear é aumentada em ln(pi), onde pi é a probabilidade anterior do grupo i. Como as observações são atribuídas a grupos pela menor distância generalizada ou pela maior função discriminante linear, o efeito é aumentar as probabilidades posteriores para um grupo com alta probabilidade anterior..
Observação
Especificar probabilidades anteriores pode afetar fortemente a precisão dos resultados. Investigue se as proporções desiguais nos grupos mostram uma diferença real na população real ou se a diferença é o resultado de um erro de amostragem.
Agora suponha que existam probabilidades anteriores e suponha que fi(x) seja a densidade conjunta para o grupo de dados i (com os parâmetros da população substituídos pelas estimativas da amostra).
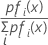
A maior probabilidade posterior é equivalente ao maior valor de ln [pifi(x)]
Se fi(x) é a distribuição normal, então:
ln [pifi(x)] = -0.5 [di2(x) – 2 ln pi] – (uma constante)
O termo entre colchetes é chamado distância quadrada generalizada de x ao grupo i e é denotada por di2(x). Observe,
di2(x) = -2[mi' Sp-1 x - 0.5 mi' Sp-1mi + ln pi] + x' Sp-1x
O termo entre colchetes é a função discriminante linear. A única diferença para o caso sem probabilidades anteriores é uma mudança no termo constante. Observe, a maior probabilidade posterior é equivalente à menor distância generalizada, que é equivalente à maior função discriminante linear.
