Contribuições de linha e de coluna para Análise de correspondência simples

Os perfis de coluna residem em um espaço c-dimensional. O conjunto completo de eixos principais d abrangem esse espaço. Suponha que g_j1, g_j2, g_j3, ..., g_jd sejam as coordenadas do perfil da coluna j em termos dos eixos principais. Essas coordenadas são chamadas de coordenadas principais da coluna. A k^ésima coordenada principal do perfil da coluna j é g_jk.

O melhor subespaço k-dimensional é cruzado pelos primeiros eixos principais k. Se projetarmos o perfil da coluna j no melhor subespaço k-dimensional, g_j1, ... g_jk são as coordenadas principais da coluna do perfil neste subespaço.

Cada eixo principal contribui para a inércia de cada linha. A correlação da linha i e o componente k, é a contribuição do eixo principal k para a inércia da linha i, expressa como uma porcentagem da inércia da linha i.

A correlação também pode ser vista como a correlação entre o perfil da linha i e o componente principal k. Esta correlação é calculada da seguinte maneira:

Similarmente, a correlação da coluna j e o componente k, é a contribuição do eixo principal k para a coluna j, expressa como uma porcentagem da inércia para a coluna j.

A correlação também pode ser vista como a correlação entre o perfil da coluna j e o componente principal k. Esta correlação é calculada da seguinte maneira:

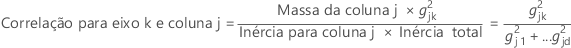
O Minitab exibe a inércia relativa de uma dada linha ou colune. A inércia absoluta é o produto da inércia relativa e da inércia total.

A soma das correlações para linha i, sobre todos os componentes principais é 1. A soma sobre as primeiras coordenadas principais k é a qualidade associada com o perfil da linha i (perfil da coluna j) e o melhor subespaço k-dimensional.

Notação

A inércia em uma célula está calculada da seguinte maneira:

A soma de todas as inércias da célula é a inércia total, algumas vezes simplesmente chamada de inércia, para a tabela.

A inércia relativa de uma célula é calculada da seguinte maneira:

Os perfis de linha residem em um espaço c-dimensional. Subespaços dimensionais inferiores são cruzados por eixos principais, também chamados de componentes principais. O primeiro eixo principal é escolhido como o vetor no espaço c-dimensional que responde pela quantidade máxima da inércia total. Portanto, o primeiro eixo principal cruza o melhor (isto é, o mais próximo dos perfis usando uma métrica adequada) subespaço 1-dimensional. O segundo eixo principal é escolhido como o vetor no espaço c-dimensional que responde pela quantidade máxima da inércia restante. Portanto, os dois primeiros eixos principais cruzam o melhor subespaço 2-dimensional. O terceiro eixo principal é escolhido como o vetor no espaço c-dimensional, após a inércia explicada pelos dois primeiros eixos principais. Portanto, os primeiros três eixos principais cruzam o melhor subespaço 3-dimensional e assim por diante.

Permita que d = o menor de (r − 1) e (c − 1). Os perfis da linha (ou equivalentemente os perfis da coluna) realmente residem em um espaço d-dimensional do espaço c-dimensional completo (ou equivalentemente o espaço r-dimensional completo). Desta forma, o número de eixos principais é, no máximo, d.

A qualidade associada ao perfil da linha i e o melhor subespaço k-dimensional são calculados da seguinte maneira:

A qualidade associada ao perfil da coluna j e o melhor subespaço k-dimensional são calculados da seguinte maneira:

A qualidade é sempre um número entre 0 e 1, com números maiores indicando uma melhor aproximação.

Notação

Cada linha contribui para a inércia de cada eixo. A contribuição da linha i para o eixo k, expresso como uma porcentagem da inércia do eixo k, é calculada da seguinte maneira:

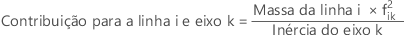
A soma das contribuições para o eixo principal k, sobre todas as linhas i, é 1.

Similarmente, cada coluna contribui para a inércia de cada eixo. A contribuição da coluna j para o eixo k, expresso como uma porcentagem da inércia do eixo k, é calculada da seguinte maneira:

A soma das contribuições para o eixo principal k, sobre todas as colunas j, é 1.

Notação

A massa da linha i é calculada da seguinte maneira:

A massa da coluna j é calculada da seguinte maneira:

O vetor das massas da linha r é o mesmo que a média do perfil da linha e o vetor das massas da coluna c é o mesmo que a média do perfil da coluna.