Neste tópico
Tabela de contingência
Suponha que uma tabela de contingência tem r linhas e c colunas. A entrada, nij, na linha i e na coluna j da tabela de contingência é a frequência daquela célula. O total na linha i, ni., é a soma das frequências na linha i. O total na coluna j, n.j, é a soma das frequências na coluna j. O total para a tabela, n.. ou apenas n, é a soma de todas as frequências na tabela.
Perfis de linha e de coluna
Os perfis são proporções calculadas das contas, nij, na tabela de contingência original. Especificamente, o perfil para a linha i é (ni1 / ni., ..., nic / ni.); o perfil para a coluna j é (n1j / n.j, ..., nrj / n.j).
O perfil de linha média é calculado do total de colunas. Especificamente, o perfil de linha média é (n.1 / n, ..., n.c / n). Similarmente, o perfil de coluna média é calculado a partir dos totais de linhas. Especificamente, o perfil de coluna média é (n1. / n,..., nr. / n).
Frequências esperadas

Valores qui-quadrado
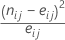
Se as frequências das células observadas e esperadas diferir muito, o valor χ2 da célula é grande.
A estatística χ2 é a soma dos valores χ2 em todas as células da tabela. Essa estatística mede a discrepância da homogeneidade dos perfis da linha, ou equivalentemente os perfis da coluna. Se os perfis da linha (coluna) forem muito diferentes um do outro, a estatística χ2 é grande. A estatística χ2 também pode ser vista como uma medida de quão distantes os perfis da linha (ou equivalentemente os perfis da coluna) estão do perfil da linha média (coluna).
Notação
| Termo | Descrição |
|---|---|
| nij | frequência observada na célula |
| eij | frequência esperada na célula |
