Neste tópico
Método de principais componentes
Na análise de componentes principais, o Minitab primeiro encontra o conjunto de autovalores ortogonais da matriz de correlação ou de covariância das variáveis. A matriz dos componentes principais é o produto da matriz de autovetores com a matriz de variáveis independentes. O primeiro componente principal é responsável pelo maior percentual da variação total de dados. O segundo componente principal é responsável pelo segundo maior percentual da variação total de dados, e assim por diante. A meta dos componentes principais é explicar a máxima quantidade de variância com o menor número de componentes.
Não unicidade de coeficientes
Os coeficientes dos componentes principais são únicos (exceto por uma mudança de sinal) se os autovalores são distintos e diferentes de zero. Se um autovalor é repetido, a "espaço abrangido" por todos os vetores dos componentes principais correspondentes ao mesmo autovalor é único, mas os vetores individuais não o são. Portanto, os coeficientes que o Minitab exibe na saída e aqueles em um livro ou outro programa podem não concordar, apesar de que os autovalores (variâncias dos componentes) serão sempre os mesmos.
Se a matriz de covariância possui posto r < p, onde p é o número de variáveis, haverá p - r autovalores iguais a zero. Os autovetores correspondentes a esses autovalores podem não ser únicos. Isso pode ocorrer se o número de observações for menor que p ou se houver multicolinearidade.
Autovetores
Os autovetores, que são compostos de coeficientes que correspondem a cada variável, são os pesos de cada variável usada para calcular os escores dos componentes principais. O autovetores são obtidos como as colunas da matriz ortogonal na decomposição espectral da matriz de covariância ou de correlação, S ou R. Mais especificamente, porque R é simétrico, existe uma matriz ortogonal V de forma que V'RV = D ou, equivalentemente, R = VDV', onde D é uma matriz diagonal cujos elementos diagonais são os autovalores. Os autovetores são as colunas de V. Os autovetores se originam de R = VDV'.
Notação
| Termo | Descrição |
|---|---|
| R | matriz de correlação |
| V | matriz de autovetores |
| D | matriz diagonal de autovalores |
Escores
Fórmula
Escores são combinações lineares das variáveis originais que respondem pela variação nos dados.
Os escores são calculados da seguinte maneira: Z = YV
Notação
| Termo | Descrição |
|---|---|
| Z | matriz dos escores dos principais componentes (n × m) |
| Y | matriz de dados padronizados (n × p) usada no método da matriz de correlação |
| V | matriz de autovalores (p × m) |
Observação
Se você usar o método da matriz de covariância em vez do método da matriz de correlação (o padrão), o Minitab usa a matriz de dados brutos para Y em vez da matriz de dados padronizados.
Autovalor
Fórmula
Os autovalores são elementos diagonais da matriz diagonal na decomposição espectral da matriz de covariância ou de correlação (consulte o tópico "Autovetores"). Os autovalores também representam as variâncias amostrais dos componentes principais Z = V Y.
Notação
| Termo | Descrição |
|---|---|
| Z | matriz dos escores dos principais componentes (n × m) |
| Y | matriz de dados padronizados (n × p) usada no método da matriz de correlação |
| V | matriz de autovalores (p × m) |
Observação
Se você usar o método da matriz de covariância em vez do método da matriz de correlação (o padrão), o Minitab usa a matriz de dados brutos para Y em vez da matriz de dados padronizados.
Proporção
Fórmula
A proporção de variância amostral explicada pelo késimo componente principal é calculada da seguinte forma:
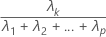
Notação
| Termo | Descrição |
|---|---|
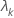 | o késimo autovalor |
| p | o número de variáveis |
Proporção acumulada
Fórmula
A proporção acumulada de variância amostral explicada pelos primeiros k componentes principais é calculada da seguinte forma: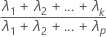
Notação
| Termo | Descrição |
|---|---|
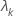 | o késimo autovalor |
| p | o número de variáveis |
Distância de Mahalanobis
Fórmula


Quando n – p – 1 é  0, o Minitab exibe o gráfico de outliers sem a linha de referência.
0, o Minitab exibe o gráfico de outliers sem a linha de referência.
Notação
| Termo | Descrição |
|---|---|
| Yi | vetor do valor de dados na linha i |
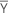 | vetor da média |
| S-1 | inverso da matriz de covariância |
| p | o número de variáveis |
| n | o número de linhas não faltantes |
