Neste tópico
Autovalor
Os autovalores (também chamados de valores característicos ou raízes latentes) são as variâncias dos componentes principais.
Interpretação
Você pode usar o tamanho do autovalor para determinar o número de componentes principais. Retenha os componentes principais com os maiores autovalores. Por exemplo, usando o critério Kaiser, você usa somente os componentes principais com os autovalores que são maiores que 1.
Para comparar visualmente o tamanho dos autovalores, use o gráfico scree. O gráfico scree pode ajudá-lo a determinar o número de componentes com base no tamanho dos autovalores.
Autoanálise (Autovalores e Autovetores) da Matriz de Correlação
| Autovalor | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proporção | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Acumulado | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Autovetores
| Variável | CP1 | CP2 | CP3 | CP4 | CP5 | CP6 | CP7 | CP8 |
|---|---|---|---|---|---|---|---|---|
| Renda | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Grau de instrução | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Idade | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Residência | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emprego | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Poupança | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Dívida | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartões de crédito | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
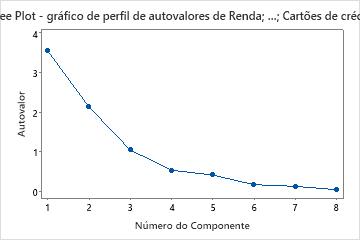
Nesses resultados, os primeiros três componentes principais têm autovalores maiores do que 1. Esses três componentes explicam 84,1% da variação nos dados. O gráfico scree mostra que os autovalores começam a formar uma linha reta após o terceiro componente principal. Se 84,1% é uma quantidade adequada de variação explicada nos dados, você deve usar os primeiros três componentes principais.
Proporção
A proporção é a proporção da variabilidade dos dado que cada componente principal explica.
Interpretação
Você pode usar a proporção para determinar quais componentes principais explicam a maioria da variabilidade nos dados. Quanto maior a proporção, mais variabilidade que o componente principal explica. O tamanho da proporção pode ajudá-lo a decidir se o componente principal é importante o suficiente para reter.
Por exemplo, um componente principal com uma proporção de 0,621 explica 62,1% da variabilidade nos dados. Portanto, é importante incluir este componente. Outro componente tem uma proporção de 0,005 e, assim explica apenas 0,5% da variabilidade nos dados. Este componente pode não ser importante o suficiente para ser incluído.
Acumulado
Acumulado é a proporção acumulada da variabilidade amostral explicada pelos componentes principais consecutivos.
Interpretação
Use a proporção acumulada para avaliar a quantidade total de variância que os componentes principais consecutivos explicam. A proporção acumulada pode ajudá-lo a determinar o número de componentes principais a ser usado. Retenha os componentes principais que explicam um nível aceitável de variância. O nível aceitável depende da sua aplicação.
Por exemplo, você pode necessitar de apenas 80% da variância explicada pelos componentes principais se você os estiver usando apenas para fins descritivos. Contudo, se quiser realizar outras análises nos dados, você deve ter, no mínimo, 90% da variância explicada pelos componentes principais.
Principais componentes (PC)
Observação
Se você usar a matriz de correlação, deverá padronizar as variáveis para obter o escore do componente correto.
Interpretação
Para interpretar cada componente principal, examine a magnitude e a direção dos coeficientes das variáveis originais. Quanto maior o valor absoluto do coeficiente, mais importante será a variável correspondente ao calcular o componente. Quão grande o valor absoluto de um coeficiente precisa ser a fim de que sua importância seja considerada subjetiva. Use seu conhecimento especializado para determinar em que nível o valor da correlação é importante.
Autoanálise (Autovalores e Autovetores) da Matriz de Correlação
| Autovalor | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proporção | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Acumulado | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Autovetores
| Variável | CP1 | CP2 | CP3 | CP4 | CP5 | CP6 | CP7 | CP8 |
|---|---|---|---|---|---|---|---|---|
| Renda | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Grau de instrução | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Idade | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Residência | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emprego | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Poupança | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Dívida | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartões de crédito | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
Nesses resultados, o primeiro componente principal tem grandes associações positivas com Idade, Residência, Emprego e Economias. Você pode interpretar este componente como sendo principalmente uma medição de uma estabilidade financeira de longo prazo do candidato. O segundo componentes tem grandes associações negativas com Cartões de débito e de crédito, portanto, este componentes mede principalmente o histórico de crédito de um candidato. O terceiro componente tem grandes associações negativas com renda, educação e cartões de crédito, de forma que este componente mede principalmente as qualificações acadêmicas e de renda de um candidato.
Escores
Os escores são combinações lineares dos dados que são determinados pelos coeficientes para cada componente principal. Para obter o escore de uma observação, substitua seus valores na equação linear pelo componente principal. Se você usar a matriz de correlação, deverá padronizar as variáveis para obter o escore do componente correto ao usar a equação linear.
Observação
Para obter o escore calculado de cada observação, clique em Armazenamento e insira uma coluna para armazenar os escores na worksheet quando você realizar a análise. Para exibir visualmente os escores para o primeiro e o segundo componentes em um gráfico, clique em Gráficos e selecione o gráfico de escores quando você realizar a análise.
Autoanálise (Autovalores e Autovetores) da Matriz de Correlação
| Autovalor | 3,5476 | 2,1320 | 1,0447 | 0,5315 | 0,4112 | 0,1665 | 0,1254 | 0,0411 |
|---|---|---|---|---|---|---|---|---|
| Proporção | 0,443 | 0,266 | 0,131 | 0,066 | 0,051 | 0,021 | 0,016 | 0,005 |
| Acumulado | 0,443 | 0,710 | 0,841 | 0,907 | 0,958 | 0,979 | 0,995 | 1,000 |
Autovetores
| Variável | CP1 | CP2 | CP3 | CP4 | CP5 | CP6 | CP7 | CP8 |
|---|---|---|---|---|---|---|---|---|
| Renda | 0,314 | 0,145 | -0,676 | -0,347 | -0,241 | 0,494 | 0,018 | -0,030 |
| Grau de instrução | 0,237 | 0,444 | -0,401 | 0,240 | 0,622 | -0,357 | 0,103 | 0,057 |
| Idade | 0,484 | -0,135 | -0,004 | -0,212 | -0,175 | -0,487 | -0,657 | -0,052 |
| Residência | 0,466 | -0,277 | 0,091 | 0,116 | -0,035 | -0,085 | 0,487 | -0,662 |
| Emprego | 0,459 | -0,304 | 0,122 | -0,017 | -0,014 | -0,023 | 0,368 | 0,739 |
| Poupança | 0,404 | 0,219 | 0,366 | 0,436 | 0,143 | 0,568 | -0,348 | -0,017 |
| Dívida | -0,067 | -0,585 | -0,078 | -0,281 | 0,681 | 0,245 | -0,196 | -0,075 |
| Cartões de crédito | -0,123 | -0,452 | -0,468 | 0,703 | -0,195 | -0,022 | -0,158 | 0,058 |
Nesses resultados, o escore do primeiro componente principal pode ser calculado dos dados padronizados, usando-se os coeficientes listados em PC1:
PC1 = 0,314 Renda + 0,237 Histórico escolar + 0,484 Idade + 0,466 Residência + 0,459 Emprego + 0,404 Economias - 0,067 Dívida - 0,123 Cartões de crédito
Distâncias
A distância de Mahalanobis é a distância entre um ponto de dados e o centróide do espaço multivariado (a média geral).
Observação
Para calcular a distância de cada observação, clique em Armazenamento e insira uma coluna na worksheet para armazenar as distâncias quando você realizar a análise. Para exibir as distâncias em um gráfico, clique em Gráficos e selecione o gráfico de outliers quando você realizar a análise.
Interpretação
Use a distância de Mahalanobis para identificar outliers. Examinar a distância de Mahalanobis é um método multivariado mais poderoso para detecção de outliers do que examinar uma variável de cada vez, porque a distância considera as diferentes escalas entre as variáveis e as correlações entre elas.
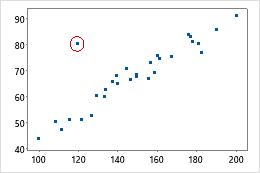
Por exemplo, quando considerados individualmente, o valor x ou o valor y do ponto de dados circundados é atípico. Contudo, o ponto de dados não se ajusta na estrutura de correlação das duas variáveis. Portanto, a distância de Mahalanobis para esse ponto é atipicamente grande.
Para avaliar se um valor da distância é grande o bastante para a observação ser considerada um outlier, use o gráfico de outliers.
Gráfico scree
O gráfico scree exibe o número do componente principal versus seu autovalor correspondente. O gráfico scree ordena os autovalores do maior para o menor. Os autovalores da matriz de correlação se igualam às variâncias dos componentes principais.
Para exibir o gráfico scree, clique em Gráficos e selecione o gráfico scree quando realizar a análise.
Interpretação

Este gráfico scree mostra que os autovalores começam a formar uma linha reta após o terceiro componente principal. Portanto, os componentes principais restantes respondem por uma proporção muito pequena da variabilidade (próximo de zero) e são provavelmente sem importância.
Gráfico de escores
O gráfico de escores representa os escores do segundo componente principal versus os escores do primeiro componente principal.
Para exibir o gráfico de escores, clique em Gráficos e selecione o gráfico de escores quando realizar a análise.
Interpretação
Se os primeiros dois componentes forem responsáveis pela maior parte da variância nos dados, você pode usar o gráfico de escores para avaliar a estrutura de dados e detectar agrupamentos, outliers e tendências. Agrupamentos de dados no gráfico podem indicar duas ou mais distribuições separadas nos dados. Se os dados seguem uma distribuição normal e não houver nenhum outlier presente, os pontos são aleatoriamente distribuídos em torno de zero.
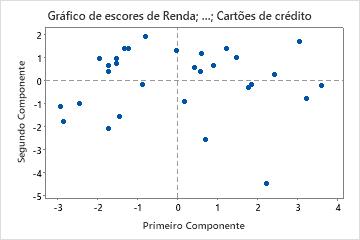
Neste gráfico de escores, o ponto no canto inferior pode ser um outlier. Você deve investigar este ponto.
Dica
Para ver o escore calculado de cada observação, mantenha o ponteiro sobre um ponto de dados no gráfico. Para criar gráficos de escores para outros componentes, armazene os escores e use .
Gráfico de cargas fatoriais
Os gráficos de cargas fatoriais representam os coeficientes de cada variável para o primeiro componente versus os coeficientes para o segundo componente. Os coeficientes são os valores que compõem os autovetores para cada componente principal. Os coeficientes indicam o peso relativo de cada variável no componente.
Para exibir o gráfico de cargas fatoriais, clique em Gráficos e selecione o gráfico de cargas fatoriais quando realizar a análise.
Interpretação
Use o gráfico de cargas fatoriais para identificar quais variáveis têm o maior efeito em cada componente. Os coeficientes podem variar de -1 a 1. Coeficientes próximos a -1 ou 1 indicam que a variável influencia fortemente o componente. Coeficientes próximos a 0 indicam que a variável tem fraca influência sobre o componente. A avaliação dos coeficientes também pode ajudar a caracterizar cada componente em termos de variáveis.
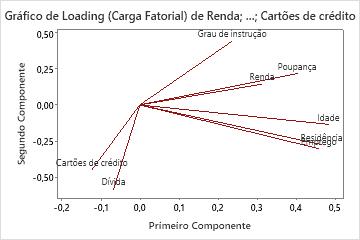
Neste gráfico de cargas fatoriais: Idade, Residência, Emprego e Economias têm grandes cargas fatoriais positivas no componente 1, portanto este componente mede principalmente a estabilidade financeira do candidato. Dívidas e cartões de crédito têm grandes coeficientes negativos no componente 2, portanto, esse componente mede principalmente o histórico de crédito de um solicitante.
Biplot
O biplot sobrepõe o gráfico de escores e o gráfico de cargas fatoriais.
Para exibir o biplot, você deve clicar em Gráficos e selecionar o biplot quando realizar a análise.
Interpretação
Use o biplot para avaliar a estrutura dos dados e as cargas fatoriais dos primeiros dois componentes em um gráfico. O Minitab representa graficamente os escores do componente principal versus os escores do primeiro componente principal, bem como as cargas fatoriais de ambos os componentes.
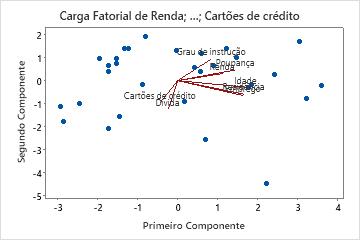
- Idade, Residência, Emprego e Economias têm grandes cargas fatoriais positivas no componente 1. Portanto, este componente enfoca na estabilidade financeira de longo prazo do candidato.
- Dívidas e Cartões de Crédito têm grandes cargas fatoriais negativas no componente 2. Portanto, este componente enfoca no histórico de crédito de um candidato.
- O ponto no canto inferior direito pode ser um outlier. Você deve investigar este ponto.
Gráfico de outlier
O gráfico de outliers exibe a distância de Mahalanobis para cada observação e uma linha de referência para identificar outliers. A distância de Mahalanobis é a distância entre cada ponto de dados e o centroide de espaço multivariado (a média geral). Examinar as distâncias de Mahalanobis é um método mais poderoso para detecção de outliers do que examinar uma variável de cada vez, porque ele considera as diferentes escalas entre as variáveis e as correlações entre elas.
Para exibir o gráfico de outliers, você deve clicar em Gráficos e selecionar o gráfico de outliers quando realizar a análise.
Interpretação
Use o gráfico de outliers para identificar outliers. Qualquer ponto que está acima da linha de referência é um outlier.
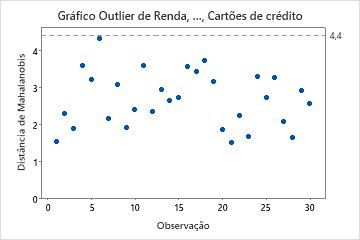
Nesses resultados, não há outliers. Todos os pontos estão abaixo da linha de referência.
Dica
Mantenha o ponteiro sobre qualquer ponto em um gráfico de outliers para identificar a observação. Use para aplicar a Função Brush em múltiplos outliers no gráfico e a de função de sinalizador nas observações na worksheet.
