Neste tópico
Etapa 1: Determinar o número de componentes principais
Use a proporção de inércia para determinar o número mínimo de componentes principais, também chamados de eixos principais, que respondem pela maioria do desvio dos valores esperados nos dados. Retenha os componentes principais que explicam um proporção aceitável da inércia total. O nível aceitável depende da sua aplicação. Idealmente, o primeiro, dois ou três componentes respondem pela maior parte da inércia total.
Se o número mínimo de componentes principais necessários não correspondem ao número de componentes que você inseriu para a análise, repita a análise usando o número adequado de componentes.
Análise da Matriz de Indicadores
| Eixo | Inércia | Proporção | Acumulado | Histograma |
|---|---|---|---|---|
| 1 | 0,4032 | 0,4032 | 0,4032 | ****************************** |
| 2 | 0,2520 | 0,2520 | 0,6552 | ****************** |
| 3 | 0,1899 | 0,1899 | 0,8451 | ************** |
| 4 | 0,1549 | 0,1549 | 1,0000 | *********** |
| Total | 1,0000 |
Principais resultados: eixos, proporção, proporção acumulada
Esses resultados mostram a decomposição da inércia total em 4 componentes. A inércia total explicada pelos quatro componentes é 1.000. Da inércia total, o primeiro componente (eixo) responde por 40,32% da inércia e o segundo componente responde por 25,20% da inércia. Juntos, esses 2 componentes respondem por 65,52% da inércia total. Portanto, especificar 2 componentes para a análise pode não ser suficiente. Adicionar um 3o. componente aumenta a proporção acumulada da inércia para 84,51%.
Etapa 2: Interpretar os componentes principais
Use os valores de qualidade para determinar a proporção de inércia representada pelos componentes de cada categoria. A qualidade é sempre um número entre 0 e 1. Valores maiores da qualidade indicam que a categoria é bem representada pelos componentes. Valores menores indicam representação inferior. Os valores da qualidade ajudam você a interpretar os componentes.
Use os valores de contribuição das colunas para avaliar quais categorias contribuem mais para a inércia de cada componente. Use o gráfico de colunas para interpretar visualmente os componentes.
Análise da Matriz de Indicadores
| Eixo | Inércia | Proporção | Acumulado | Histograma |
|---|---|---|---|---|
| 1 | 0,4032 | 0,4032 | 0,4032 | ****************************** |
| 2 | 0,2520 | 0,2520 | 0,6552 | ****************** |
| 3 | 0,1899 | 0,1899 | 0,8451 | ************** |
| 4 | 0,1549 | 0,1549 | 1,0000 | *********** |
| Total | 1,0000 |
Contribuições de Coluna
| Componente 1 | Componente 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | Nome | Qual | Massa | Inerte | Coord | Corr | Contr | Coord | Corr | Contr |
| 1 | Pequeno | 0,9655 | 0,0424 | 0,2076 | 0,3814 | 0,0297 | 0,0153 | -2,1394 | 0,9357 | 0,7707 |
| 2 | Padrão | 0,9655 | 0,2076 | 0,0424 | -0,0780 | 0,0297 | 0,0031 | 0,4374 | 0,9357 | 0,1576 |
| 3 | SemEjeção | 0,4739 | 0,2134 | 0,0366 | -0,2844 | 0,4717 | 0,0428 | -0,0197 | 0,0023 | 0,0003 |
| 4 | Ejeção | 0,4739 | 0,0366 | 0,2134 | 1,6587 | 0,4717 | 0,2497 | 0,1151 | 0,0023 | 0,0019 |
| 5 | Colis | 0,6133 | 0,1926 | 0,0574 | -0,4264 | 0,6095 | 0,0868 | 0,0338 | 0,0038 | 0,0009 |
| 6 | Capotagem | 0,6133 | 0,0574 | 0,1926 | 1,4294 | 0,6095 | 0,2911 | -0,1133 | 0,0038 | 0,0029 |
| 7 | NãoGrave | 0,5680 | 0,1353 | 0,1147 | -0,6523 | 0,5018 | 0,1428 | -0,2371 | 0,0663 | 0,0302 |
| 8 | Grave | 0,5680 | 0,1147 | 0,1353 | 0,7692 | 0,5018 | 0,1684 | 0,2795 | 0,0663 | 0,0356 |
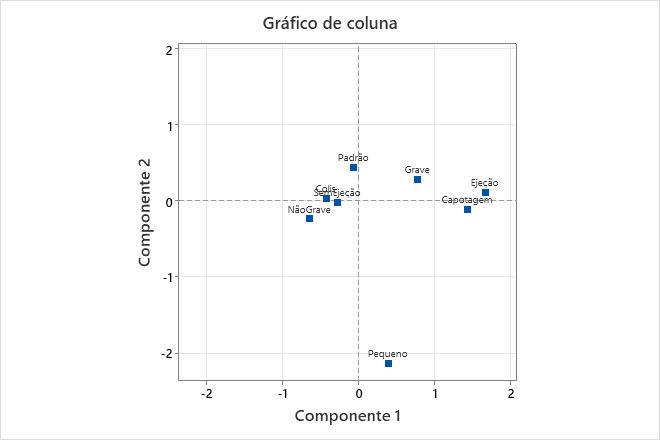
Principais resultados: Qual, Contr, Gráfico de colunas
Nesta análise, o Minitab calcula dois principais componentes dos dados relacionados a acidentes de carro. Na tabela Contribuições da coluna, os valores da qualidade superiores ocorrem para tamanhos de carro pequeno (0,965) e Padrão (0,965). Portanto, essas duas categorias são melhores representadas pelos dois componentes. A gravidade do acidente tem a representação inferior, com um valor da qualidade de 0,568 para Grave e NãoGrave. Capotagem (0,291) e Ejeção (0,250) contribuem o máximo para a inércia do Componente 1. Os tamanhos dos carros Pequenos (0,771) e Padrão (0,158) contribuem o máximo para a inércia do Componente 2. Contudo, esses resultados devem ser interpretados com cuidado, porque dois componentes podem não explicar adequadamente a variabilidade desses dados.
O gráfico de colunas mostra as coordenadas principais das colunas. O Componente 1 explica melhor a Capotagem e a Ejeção com essas duas categorias mais distantes da origem no eixo horizontal. Grave e NãoGrave estão em lados opostos da origem no eixo horizontal. Portanto, o componente 1 contrasta esses valores de categoria. O componente 2 é mostrado no eixo vertical. O componente 2 explica melhor o tamanho de carro pequeno, e o contrasta com as outras categorias.
Etapa 3: Examinar a inércia das categorias
Examinar os valores de inércia calculados para as categorias de colunas. As categorias que se desviam mais de seu valor esperado têm um valor de inércia mais alto e contribuem mais para o valor qui-quadrado total.
Contribuições de Coluna
| Componente 1 | Componente 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | Nome | Qual | Massa | Inerte | Coord | Corr | Contr | Coord | Corr | Contr |
| 1 | Pequeno | 0,9655 | 0,0424 | 0,2076 | 0,3814 | 0,0297 | 0,0153 | -2,1394 | 0,9357 | 0,7707 |
| 2 | Padrão | 0,9655 | 0,2076 | 0,0424 | -0,0780 | 0,0297 | 0,0031 | 0,4374 | 0,9357 | 0,1576 |
| 3 | SemEjeção | 0,4739 | 0,2134 | 0,0366 | -0,2844 | 0,4717 | 0,0428 | -0,0197 | 0,0023 | 0,0003 |
| 4 | Ejeção | 0,4739 | 0,0366 | 0,2134 | 1,6587 | 0,4717 | 0,2497 | 0,1151 | 0,0023 | 0,0019 |
| 5 | Colis | 0,6133 | 0,1926 | 0,0574 | -0,4264 | 0,6095 | 0,0868 | 0,0338 | 0,0038 | 0,0009 |
| 6 | Capotagem | 0,6133 | 0,0574 | 0,1926 | 1,4294 | 0,6095 | 0,2911 | -0,1133 | 0,0038 | 0,0029 |
| 7 | NãoGrave | 0,5680 | 0,1353 | 0,1147 | -0,6523 | 0,5018 | 0,1428 | -0,2371 | 0,0663 | 0,0302 |
| 8 | Grave | 0,5680 | 0,1147 | 0,1353 | 0,7692 | 0,5018 | 0,1684 | 0,2795 | 0,0663 | 0,0356 |
Principais resultados: Inércia da coluna
Na tabela Contribuições da coluna, a coluna rotulada Inerte é a proporção da inércia total contribuída por cada categoria. Assim, a Ejeção desvia mais de seu valor esperado e contribui com 21,3% do total das estatísticas qui-quadrado.
