Neste tópico
Principais componentes
No método de extração dos principais componentes, as jésimas cargas fatoriais são os coeficientes escalados dos jésimos principais componentes. Os fatores são relacionados aos primeiros m componentes. Na solução não rotacionada, você pode interpretar os fatores como você interpretaria os componentes na análise dos principais componentes. Contudo, após a rotação, você não pode mais interpretar os fatores similares aos principais componentes.
A análise fatorial do principal componente da matriz de correlação amostral R (ou matriz de covariância S) está especificada em termos de seus pares autovalor-autovetor (λi, ei), i = 1, ...,p e λ1 ≤ λ2 ≤ ... ≤ λp. Deixe que m < p seja o número de fatores comuns. A matriz de cargas fatoriais estimada é uma matriz p × m, L, cuja iésima coluna é  , i = 1, ..., m.
, i = 1, ..., m.
Máxima verossimilhança
O método da máxima verossimilhança estima as cargas fatoriais, supondo-se que os dados seguem uma distribuição normal multivariada. Conforme seu nome indica, este método encontra estimativas das cargas fatoriais e variâncias únicas maximizando a função de verossimilhança associada com o modelo normal multivariado. Equivalentemente, isso é feito ao minimizar-se uma expressão envolvendo as variâncias dos resíduos. O algoritmo intera até um mínimo ser encontrado ou até que o número máximo especificado de iterações (o padrão é 25) seja alcançado.
O Minitab usa um algoritmo baseado em Joreskog,1,2 com alguns ajustes para aprimorar a convergência. Damos um breve resumo do algoritmo aqui.
Suponha que temos p variáveis e queremos ajustar um modelo com m fatores. Permita que o R seja a matriz de correlação p × p das variáveis, L seja a matriz p × m de cargas fatoriais, e Ψ seja uma matriz diagonal p × p cujos elementos diagonais são variâncias únicas, Ψi. Depois, precisamos encontrar valores para L e Ψ que maximizam a função da verossimilhança, f(L,Ψ). Isso envolve um procedimento de duas etapas, primeiro encontrar um valor para Ψ, depois para L.
Você pode indiretamente especificar o valor inicial de Ψ. Na subcaixa de diálogo Análise Fatorial - Opções, insira a coluna que contém os valores iniciais das comunalidades em Usar estimativas comuns iniciais em. O Minitab então calcula os elementos diagonais de Ψ como (1 − comunalidades).
Para um valor fixo de Ψ, maximizamos f(L,Ψ) com respeito a L. Este é um cálculo de matriz simples. O valor de L é então substituído por f(L,Ψ). Agora f pode ser exibido como uma função de Ψ. Uma simples transformação desta função dá
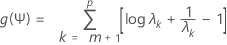
onde λ1 < λ2 < ... λp são autovalores de Ψ R- 1Ψ. Depois minimizamos g(Ψ), usando um procedimento de Newton-Raphson. Isso dá uma estimativa de Ψ, que é então substituído na verossimilhança f(L,Ψ). Então a verossimilhança é novamente maximizada com respeito a L. Depois, um novo valor de g(Ψ) é calculado, e assim por diante. Por padrão, as iterações continuam até 25 passos se a convergência não for alcançada. Se o algoritmo não convergir em 25 passos, mude o número máximo padrão de iterações na subcaixa de diálogo Opções.
A convergência é alcançada na etapa n, se um dos seguintes for verdadeiro:
- A função g(Ψ) não muda muito entre passos consecutivos. Especificamente, se:
- | [g(Ψ) no passo n] − [g(Ψ) no passo (n − 1)] | < 10-6
- Nenhuma das variâncias únicas muda muito entre passos consecutivos. Especialmente, se:
- | ln(Ψi no passo n) − ln(Ψi no passo n − 1) | < K2,
para todos i = 1, ... , p, onde Ψi o iésimo elemento diagonal de Ψ, é a variância exclusiva que corresponde à variável i.
O valor de K2 pode ser especificado em Convergência na subcaixa de diálogo Opções. Por padrão, o valor é 0,005.
EscolhaTodos e iterações de MLE na subcaixa de diálogo Resultados para exibir as informações em cada iteração. O valor da função objetiva, g(Ψ), é exibido, depois a mudança máxima em ln(Ψi). Se, em uma iteração, o valor de g(Ψ) não diminuir, um passo menor (metade do tamanho) será tomado. O meio passo é continuado até g(Ψ) diminuir ou 25 meio passos serem dados. O número de meio passos é exibido. Se g(Ψ) não tiver diminuído em 25 meio passos, o algoritmo para e uma mensagem é exibida.
Uma matriz de segundos derivados é usada na minimização de g(Ψ). Esta matriz nem sempre é definida positiva. Se ela não for, será usada uma aproximação. Um asterisco é exibido nos resultados quando o Minitab usa a matriz exata.
Ao minimizar a função g(Ψ), é possível encontrar valores do elemento diagonal de Ψ que são 0 ou negativo. Para impedir isso, o algoritmo do Minitab limita os elementos diagonais de Ψ longe de 0. Especificamente, se uma variância única Ψi for menor que K2, ela é definida igual a K2. K2 é o valor definido em Convergência na subcaixa de diálogo Opções.
Quando o algoritmo converge, é realizada uma verificação final nas variâncias únicas. Se quaisquer das variâncias únicas for menor que K2, elas são definidas igual a 0. A comunalidade correspondente é igual a 1. Este resultado é chamado de caso Heywood e o Minitab exibe uma mensagem para informar o usuário deste resultado. Os algoritmos de otimização, como o utilizado para análise fatorial de máxima verossimilhança, podem dar diferentes respostas com mudanças pequenas na entrada. Por exemplo, se você mudar alguns pontos de dados, mude os valores iniciais em Usar estimativas comuns iniciais em, ou mude o critério de convergência em Convergência, você pode ver diferenças nos resultados da análise fatorial. Isso é especialmente verdadeiro se a solução reside em um local relativamente plano na superfície da máxima verossimilhança.
Rotação de cargas fatoriais
Uma rotação ortogonal é uma transformação ortogonal das cargas fatoriais que permitem uma interpretação mais fácil das cargas fatoriais. As cargas fatoriais rotacionadas retêm a matriz de correlação ou de covariância, a matriz de resíduos, as variâncias específicas e as comunalidades. Como as cargas fatoriais mudam, a variância contabilizada por cada fator e a proporção correspondente mudam.
A rotação coloca os eixos próximos ao máximo de pontos possível e associa cada grupo de variáveis com um fator. Contudo, em alguns casos, uma variável está perto de mais de um eixo e está, portanto, associada com mais de um fator.
Você pode escolher entre quatro métodos de rotação:
- Equimax - maximiza a variância de cargas fatoriais quadráticas dentro de variáveis e fatores.
- Varimax - maximiza a variância de cargas fatoriais quadráticas dentro de fatores. Este método simplifica as colunas da matriz de cargas fatoriais e é o método de rotação mais amplamente utilizado. Para facilitar a interpretação, este método tenta tornar as cargas fatoriais grandes ou pequenas.
- Quartimax - maximiza a variância de cargas fatoriais quadráticas dentro de variáveis. Este método simplifica as linhas da matriz de cargas fatoriais.
- Ortomax com γ - rotação que compreende os três acima, dependendo do valor gama do parâmetro (0 - 1).
Modelo de análise fatorial
O modelo de análise fatorial é:
X = μ + L F + e
onde X é o vetor de medições p x 1, μ é o vetor de médias p x 1, L é uma matriz de cargas fatoriais p × m, F é um vetor de fatores comuns m × 1, e e é um vetor de resíduos p × 1. Aqui, p representa o número de medições em um sujeito ou item e m representa o número de fatores comuns. Supõe-se que F e e sejam independentes e que os Fs do indivíduo sejam independentes entre si. A média de F e e é 0, Cov(F) = I, a matriz de identidade e Cov(e) = Ψ, uma matriz diagonal. As suposições sobre independência dos Fs torna este um modelo de fator ortogonal.
Sob o modelo de análise fatorial, a matriz de covariância p x p dos dados, X, é calculada da seguinte forma:
Cov(X) = L L' + Ψ
onde L é a matriz de cargas fatoriais p × m, e Ψ é uma matriz diagonal p × p. O iésimo elemento diagonal de L L', a soma das cargas fatoriais quadráticas, é chamada de iésima comunalidade. Os valores da comunalidade podem ser julgados como o percentual da variabilidade explicado pelos fatores comuns. O iésimo elemento diagonal de Ψ é chamado de iésima variância específica ou singularidade. A variância específica é aquela porção da variabilidade não explicada pelos fatores comuns. Os tamanhos das comunalidades e/ou das variâncias específicas podem ser usados para avaliar a qualidade do ajuste.
Cargas fatoriais
Fórmula
Quando o método de componentes principais é usado, a matriz de cargas fatoriais estimadas, L, é dada por:
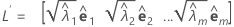
Quando o método da máxima verossimilhança é usado, a matriz de cargas fatoriais é obtida através de um processo iterativo.
Notação
| Termo | Descrição |
|---|---|
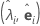 | pares de autovalor-autovetor |
Comunalidades
Fórmula
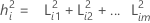
onde i = 1, 2 ... p
Notação
| Termo | Descrição |
|---|---|
| L | matriz de cargas fatoriais |
Variância
A variabilidade nos dados explicada por cada fator. A variância é igual ao autovalor se você usar os componentes principais para extrair fatores e não rotacionar as cargas.
% Var
Fórmula
Quando uma matriz de correlação é usada, a proporção da variância explicada pelo jésimo fator é calculada da seguinte forma:
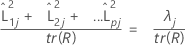
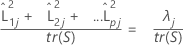
Notação
| Termo | Descrição |
|---|---|
| L | matriz de cargas fatoriais |
| λj | jésimo autovalor |
| tr(R) | traço da matriz de correlação |
| tr(S) | traço da matriz de covariância |
Coeficientes
Fórmula
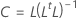
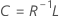
R é a matriz de correlação. Se a matriz do fator é a matriz de covariância, R é substituído pela matriz de covariância.
Notação
| Termo | Descrição |
|---|---|
| L | matriz de cargas fatoriais |
Escores
Fórmula
F = ZC
Notação
| Termo | Descrição |
|---|---|
| F | matriz de escores fatoriais |
| Z | dados padronizados |
| C | matriz de coeficientes de escores fatoriais |
