Neste tópico
Etapa 1: determinar o número de fatores
- % Var
- Use a porcentagem da variância (% Var) para determinar a quantidade de variância que os fatores explicam. Retenha os fatores que explicam um nível aceitável de variância. O nível aceitável depende da sua aplicação. Para fins descritivos, você pode necessitar de apenas 80% da variância explicada. Contudo, se quiser realizar outras análises nos dados, você deve ter, no mínimo, 90% da variância explicada pelos fatores.
- Variância (autovalores)
- A variância é igual ao autovalor se você usar os componentes principais para extrair fatores e não rotacionar as cargas. Você pode usar o tamanho do autovalor para determinar o número de fatores. Retenha os fatores com os maiores autovalores. Por exemplo, usando o critério Kaiser, você usa somente os fatores com os autovalores que são maiores que 1.
- Gráfico scree
- O gráfico scree ordena os autovalores do maior para o menor. O padrão ideal é uma curva acentuada, seguida de uma dobra e depois de uma linha reta. Use os componentes na curva acentuada antes do primeiro ponto que inicia a tendência da linha.
Cargas Fatoriais Não Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Fator5 | Fator6 | Fator7 | Fator8 | Fator9 |
|---|---|---|---|---|---|---|---|---|---|
| Histórico Escolar | 0,726 | 0,336 | -0,326 | 0,104 | -0,354 | -0,099 | 0,233 | 0,147 | 0,097 |
| Aparência | 0,719 | -0,271 | -0,163 | -0,400 | -0,148 | -0,362 | -0,195 | -0,151 | 0,082 |
| Comunicação | 0,712 | -0,446 | 0,255 | 0,229 | -0,319 | 0,119 | 0,032 | 0,088 | 0,023 |
| Adaptação à Empresa | 0,802 | -0,060 | 0,048 | 0,428 | 0,306 | -0,137 | -0,067 | 0,105 | -0,019 |
| Experiência | 0,644 | 0,605 | -0,182 | -0,037 | -0,092 | 0,317 | -0,209 | -0,102 | 0,121 |
| Adaptação ao Trabalho | 0,813 | 0,078 | -0,029 | 0,365 | 0,368 | -0,067 | -0,025 | -0,032 | 0,146 |
| Carta | 0,625 | 0,327 | 0,654 | -0,134 | 0,031 | 0,025 | 0,017 | -0,113 | -0,079 |
| Simpatia | 0,739 | -0,295 | -0,117 | -0,346 | 0,249 | 0,140 | 0,353 | -0,142 | 0,051 |
| Organização | 0,706 | -0,540 | 0,140 | 0,247 | -0,217 | 0,136 | -0,080 | -0,105 | -0,020 |
| Potencial | 0,814 | 0,290 | -0,326 | 0,167 | -0,068 | -0,073 | 0,048 | -0,112 | -0,290 |
| Currículo | 0,709 | 0,298 | 0,465 | -0,343 | -0,022 | -0,107 | 0,024 | 0,170 | 0,008 |
| Autoconfiança | 0,719 | -0,262 | -0,294 | -0,409 | 0,175 | 0,179 | -0,159 | 0,230 | -0,098 |
| Variância | 6,3876 | 1,4885 | 1,1045 | 1,0516 | 0,6325 | 0,3670 | 0,3016 | 0,2129 | 0,1557 |
| % de Var | 0,532 | 0,124 | 0,092 | 0,088 | 0,053 | 0,031 | 0,025 | 0,018 | 0,013 |
| Variável | Fator10 | Fator11 | Fator12 | Comum |
|---|---|---|---|---|
| Histórico Escolar | -0,142 | -0,026 | -0,031 | 1,000 |
| Aparência | 0,016 | 0,020 | -0,038 | 1,000 |
| Comunicação | 0,204 | 0,012 | -0,100 | 1,000 |
| Adaptação à Empresa | -0,067 | 0,188 | -0,021 | 1,000 |
| Experiência | 0,039 | 0,077 | 0,009 | 1,000 |
| Adaptação ao Trabalho | 0,066 | -0,176 | 0,008 | 1,000 |
| Carta | -0,130 | -0,043 | -0,127 | 1,000 |
| Simpatia | 0,022 | 0,064 | 0,012 | 1,000 |
| Organização | -0,162 | -0,032 | 0,136 | 1,000 |
| Potencial | 0,100 | -0,023 | 0,028 | 1,000 |
| Currículo | 0,090 | 0,010 | 0,156 | 1,000 |
| Autoconfiança | -0,061 | -0,065 | -0,047 | 1,000 |
| Variância | 0,1379 | 0,0851 | 0,0750 | 12,0000 |
| % de Var | 0,011 | 0,007 | 0,006 | 1,000 |
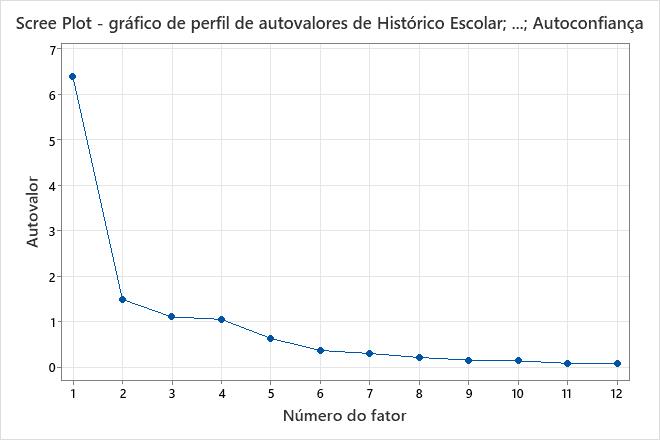
Principais resultados: %Var, variância (autovalor), gráfico scree
Esses resultados mostram as cargas fatoriais não rotacionadas para todos os fatores que usam o método de extração dos componentes principais. Os primeiros quatro fatores têm variâncias (autovalores) maiores que 1. Os autovalores mudam menos marcadamente quando mais de 6 fatores são usados. Portanto, 4–6 fatores parecem explicar a maior parte da variabilidade nos dados. A porcentagem da variabilidade explicada pelo fator 1 é 0,532 ou 53,2%. A porcentagem da variabilidade explicada pelo Fator 4 é 0,088 ou 8,8%. O gráfico scree mostra que os primeiros quatro fatores respondem pela maior parte da variabilidade total nos dados. Os fatores restantes respondem por uma proporção muito pequena da variabilidade e são provavelmente sem importância.
Etapa 2: Interpretar os fatores
Depois de você determinar o número de fatores (etapa 1), você pode repetir a análise usando o método de máxima verossimilhança. Depois examine o padrão de carga fatorial para determinar o fator que tem a maior influência em cada variável. As cargas fatoriais próximas de -1 ou 1 indicam que o fator influencia fortemente a variável. As cargas fatoriais próximas de 0 indicam que o fator tem uma influência fraca na variável. Algumas variáveis podem ter altas cargas fatoriais em múltiplos fatores.
As cargas fatoriais não rotacionadas são frequentemente difíceis de interpretar. A rotação de fatores simplifica a estrutura de cargas fatoriais, permitindo a você interpretar mais facilmente as cargas fatoriais. Contudo, um método de rotação pode não funcionar bem em todos os casos. Você deve tentar diferentes rotações e usar aquela que produz os resultados mais interpretáveis. Você também pode classificar as cargas fatoriais rotacionadas para avaliar mais claramente as cargas fatoriais dentro de um fator.
Cargas Fatoriais Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Comum |
|---|---|---|---|---|---|
| Histórico Escolar | 0,481 | 0,510 | 0,086 | 0,188 | 0,534 |
| Aparência | 0,140 | 0,730 | 0,319 | 0,175 | 0,685 |
| Comunicação | 0,203 | 0,280 | 0,802 | 0,181 | 0,795 |
| Adaptação à Empresa | 0,778 | 0,165 | 0,445 | 0,189 | 0,866 |
| Experiência | 0,472 | 0,395 | -0,112 | 0,401 | 0,553 |
| Adaptação ao Trabalho | 0,844 | 0,209 | 0,305 | 0,215 | 0,895 |
| Carta | 0,219 | 0,052 | 0,217 | 0,947 | 0,994 |
| Simpatia | 0,261 | 0,615 | 0,321 | 0,208 | 0,593 |
| Organização | 0,217 | 0,285 | 0,889 | 0,086 | 0,926 |
| Potencial | 0,645 | 0,492 | 0,121 | 0,202 | 0,714 |
| Currículo | 0,214 | 0,365 | 0,113 | 0,789 | 0,814 |
| Autoconfiança | 0,239 | 0,743 | 0,249 | 0,092 | 0,679 |
| Variância | 2,5153 | 2,4880 | 2,0863 | 1,9594 | 9,0491 |
| % de Var | 0,210 | 0,207 | 0,174 | 0,163 | 0,754 |
Principais resultados: cargas fatoriais, comunalidade, gráfico de cargas fatoriais
- Adequado para a empresa (0,778), Adequado para a função (0,844), e Potencial (0,645) têm grandes cargas fatoriais positivas no fator 1, portanto, este fator descreve uma adequação e potencial do candidato para crescimento na empresa.
- Aparência (0,73), Simpatia (0,615) e Autoconfiança (0,743) têm grandes cargas fatoriais positivas no fator 2, portanto, este fator descreve as qualidades pessoais.
- Comunicação (0,802) e Organização (0,889) têm grandes cargas fatoriais positivas no fator 3, portanto este fator descreve as habilidades de trabalho.
- Carta (0,947) e Currículo (0,789) têm grandes cargas fatoriais positivas no fator 4, portanto, este fator descreve as habilidades de escrita.
Juntos, todos os quatro fatores explicam 0,754 ou 75,4% da variação nos dados.
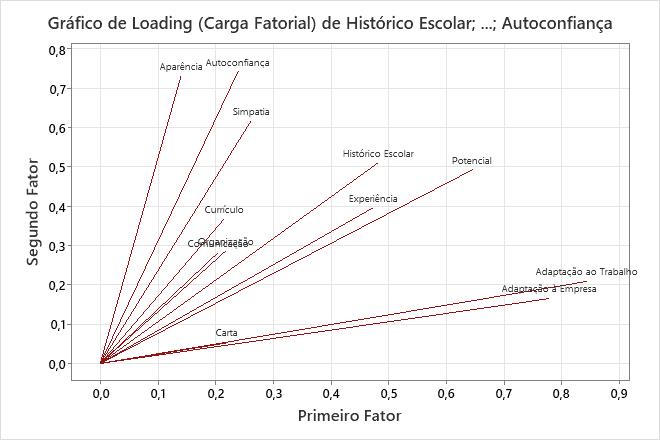
O gráfico de cargas fatoriais mostra visualmente os resultados das cargas fatoriais para os primeiros dois fatores.
Etapa 3: Verifique se há problemas nos dados
Se os primeiros dois fatores forem responsáveis pela maior parte da variância nos dados, você pode usar o gráfico de escores para avaliar a estrutura de dados e detectar agrupamentos, outliers e tendências. Agrupamentos de dados no gráfico podem indicar duas ou mais distribuições separadas nos dados. Se os dados seguem uma distribuição normal e não houver nenhum outlier presente, os pontos são aleatoriamente distribuídos sobre o valor de 0.
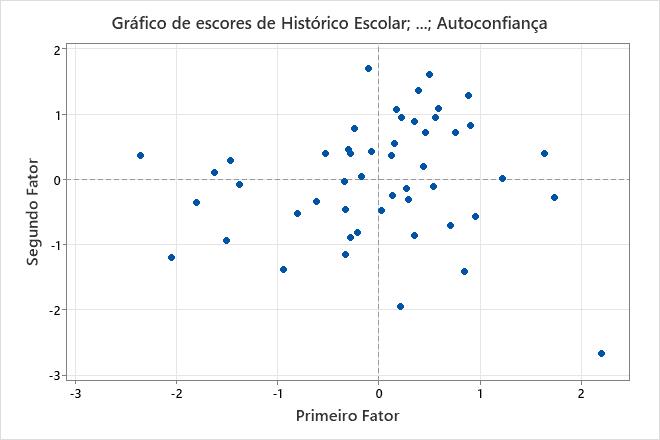
Principal resultado: gráfico de escores
Neste gráfico de escores, os dados parecem normais e não há outliers extremos aparentes. Contudo, você pode querer investigar o valor dos dados no lado direito inferior do gráfico, que se localiza longe dos outros valores de dados.
Dica
Para ver o escore calculado de cada observação, mantenha o ponteiro sobre um ponto de dados no gráfico. Para criar gráficos de escores para outros fatores, armazene os escores e use .
