Neste tópico
Cargas fatoriais
As cargas fatoriais indicam quanto um fator explica uma variável. As cargas fatoriais podem variar de -1 a 1.
O Minitab calcula cargas fatoriais não rotacionadas e cargas fatoriais rotacionadas se você selecionar um método de rotação para a análise.
Interpretação
Examine o padrão de carga fatorial para determinar o fator que tem a maior influência em cada variável. As cargas fatoriais próximas de -1 ou 1 indicam que o fator influencia fortemente a variável. As cargas fatoriais próximas de 0 indicam que o fator tem uma influência fraca na variável. Algumas variáveis podem ter altas cargas fatoriais em múltiplos fatores.
As cargas fatoriais não rotacionadas são frequentemente difíceis de interpretar. A rotação de fatores simplifica a estrutura de cargas fatoriais e frequentemente torna os fatores mais claramente distinguíveis e fáceis de interpretar. Contudo, um método de rotação pode não funcionar bem em todos os casos. Você deve tentar diferentes rotações e usar aquela que produz os resultados mais interpretáveis. Você também pode classificar as cargas fatoriais rotacionadas para avaliar mais claramente as cargas fatoriais dentro de um fator.
- Adequado para a empresa (0,778), Adequado para a função (0,844), e Potencial (0,645) têm grandes cargas fatoriais positivas no fator 1, portanto, este fator descreve uma adequação e potencial do candidato para crescimento na empresa.
- Aparência (0,730), Simpatia (0,615) e Autoconfiança (0,743) têm grandes cargas fatoriais positivas no fator 2, portanto, este fator descreve as qualidades pessoais.
- Comunicação (0,802) e Organização (0,889) têm grandes cargas fatoriais positivas no fator 3, portanto este fator descreve as habilidades de trabalho.
- Carta (0,947) e Currículo (0,789) têm grandes cargas fatoriais positivas no fator 4, portanto, este fator descreve as habilidades de escrita.
Cargas Fatoriais Não Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Comum |
|---|---|---|---|---|---|
| Histórico Escolar | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Aparência | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Comunicação | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Adaptação à Empresa | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Experiência | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Adaptação ao Trabalho | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Carta | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Simpatia | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Organização | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potencial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Currículo | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Autoconfiança | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Variância | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % de Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
Cargas Fatoriais Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Comum |
|---|---|---|---|---|---|
| Histórico Escolar | 0,481 | 0,510 | 0,086 | 0,188 | 0,534 |
| Aparência | 0,140 | 0,730 | 0,319 | 0,175 | 0,685 |
| Comunicação | 0,203 | 0,280 | 0,802 | 0,181 | 0,795 |
| Adaptação à Empresa | 0,778 | 0,165 | 0,445 | 0,189 | 0,866 |
| Experiência | 0,472 | 0,395 | -0,112 | 0,401 | 0,553 |
| Adaptação ao Trabalho | 0,844 | 0,209 | 0,305 | 0,215 | 0,895 |
| Carta | 0,219 | 0,052 | 0,217 | 0,947 | 0,994 |
| Simpatia | 0,261 | 0,615 | 0,321 | 0,208 | 0,593 |
| Organização | 0,217 | 0,285 | 0,889 | 0,086 | 0,926 |
| Potencial | 0,645 | 0,492 | 0,121 | 0,202 | 0,714 |
| Currículo | 0,214 | 0,365 | 0,113 | 0,789 | 0,814 |
| Autoconfiança | 0,239 | 0,743 | 0,249 | 0,092 | 0,679 |
| Variância | 2,5153 | 2,4880 | 2,0863 | 1,9594 | 9,0491 |
| % de Var | 0,210 | 0,207 | 0,174 | 0,163 | 0,754 |
Comunalidade
A comunalidade é a proporção de variabilidade de cada variável que é explicada pelos fatores. O valor da comunalidade é o mesmo, independentemente se você usa cargas fatoriais de fatores não rotacionados ou cargas fatoriais de fatores rotacionados para a análise.
Interpretação
Examine os valores da comunalidade para avaliar quão bem cada variável é explicada pelos fatores. Quanto mais perto a comunalidade estiver de 1, melhor a variável é explicada pelos fatores. Você pode decidir adicionar um fator se o fator contribui significativamente para o ajuste de determinadas variáveis.
Cargas Fatoriais Não Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Comum |
|---|---|---|---|---|---|
| Histórico Escolar | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Aparência | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Comunicação | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Adaptação à Empresa | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Experiência | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Adaptação ao Trabalho | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Carta | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Simpatia | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Organização | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potencial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Currículo | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Autoconfiança | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Variância | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % de Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
Nesses resultados, 4 fatores foram extraídos das 12 variáveis. Esses valores da comunalidade são geralmente altos para todas as variáveis, o que indica que as variáveis estão bem representadas pelos 4 fatores. Por exemplo, 0,895 ou 89,5%, da variabilidade em Adequado para a função é explicado pelos 4 fatores.
Variância
A variabilidade nos dados explicada por cada fator. A variância de fator é igual ao autovalor se você usar o método de extração dos componentes principais e não rotacionar as cargas fatoriais. A rotação muda a distribuição da proporção da variação explicada por cada fator, apesar de a variação total explicada por todos os fatores permanecer a mesma.
Interpretação
Examine a variância de cada fator. Quanto maior a variância, mais o fator explica a variabilidade nos dados. Se não souber quantos fatores extrair na análise, você poderá primeiro usar o método de extração dos componentes principais, sem rotação, usando o número padrão dos fatores (que extrai o número máximo de fatores) como uma avaliação preliminar. Depois defina os fatores importantes como aqueles com uma variância (autovalor) maior que um determinado valor. Por exemplo, um critério é incluir quaisquer fatores com um autovalor de, no mínimo, 1. Outro método é avaliar visualmente os autovalores no gráfico scree para determinar em que ponto os autovalores mostram um pequena mudança e abordagem 0. Para obter mais informações, consulte o tópico sobre o Gráfico scree.
Cargas Fatoriais Não Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Fator5 | Fator6 | Fator7 | Fator8 | Fator9 |
|---|---|---|---|---|---|---|---|---|---|
| Histórico Escolar | 0,726 | 0,336 | -0,326 | 0,104 | -0,354 | -0,099 | 0,233 | 0,147 | 0,097 |
| Aparência | 0,719 | -0,271 | -0,163 | -0,400 | -0,148 | -0,362 | -0,195 | -0,151 | 0,082 |
| Comunicação | 0,712 | -0,446 | 0,255 | 0,229 | -0,319 | 0,119 | 0,032 | 0,088 | 0,023 |
| Adaptação à Empresa | 0,802 | -0,060 | 0,048 | 0,428 | 0,306 | -0,137 | -0,067 | 0,105 | -0,019 |
| Experiência | 0,644 | 0,605 | -0,182 | -0,037 | -0,092 | 0,317 | -0,209 | -0,102 | 0,121 |
| Adaptação ao Trabalho | 0,813 | 0,078 | -0,029 | 0,365 | 0,368 | -0,067 | -0,025 | -0,032 | 0,146 |
| Carta | 0,625 | 0,327 | 0,654 | -0,134 | 0,031 | 0,025 | 0,017 | -0,113 | -0,079 |
| Simpatia | 0,739 | -0,295 | -0,117 | -0,346 | 0,249 | 0,140 | 0,353 | -0,142 | 0,051 |
| Organização | 0,706 | -0,540 | 0,140 | 0,247 | -0,217 | 0,136 | -0,080 | -0,105 | -0,020 |
| Potencial | 0,814 | 0,290 | -0,326 | 0,167 | -0,068 | -0,073 | 0,048 | -0,112 | -0,290 |
| Currículo | 0,709 | 0,298 | 0,465 | -0,343 | -0,022 | -0,107 | 0,024 | 0,170 | 0,008 |
| Autoconfiança | 0,719 | -0,262 | -0,294 | -0,409 | 0,175 | 0,179 | -0,159 | 0,230 | -0,098 |
| Variância | 6,3876 | 1,4885 | 1,1045 | 1,0516 | 0,6325 | 0,3670 | 0,3016 | 0,2129 | 0,1557 |
| % de Var | 0,532 | 0,124 | 0,092 | 0,088 | 0,053 | 0,031 | 0,025 | 0,018 | 0,013 |
| Variável | Fator10 | Fator11 | Fator12 | Comum |
|---|---|---|---|---|
| Histórico Escolar | -0,142 | -0,026 | -0,031 | 1,000 |
| Aparência | 0,016 | 0,020 | -0,038 | 1,000 |
| Comunicação | 0,204 | 0,012 | -0,100 | 1,000 |
| Adaptação à Empresa | -0,067 | 0,188 | -0,021 | 1,000 |
| Experiência | 0,039 | 0,077 | 0,009 | 1,000 |
| Adaptação ao Trabalho | 0,066 | -0,176 | 0,008 | 1,000 |
| Carta | -0,130 | -0,043 | -0,127 | 1,000 |
| Simpatia | 0,022 | 0,064 | 0,012 | 1,000 |
| Organização | -0,162 | -0,032 | 0,136 | 1,000 |
| Potencial | 0,100 | -0,023 | 0,028 | 1,000 |
| Currículo | 0,090 | 0,010 | 0,156 | 1,000 |
| Autoconfiança | -0,061 | -0,065 | -0,047 | 1,000 |
| Variância | 0,1379 | 0,0851 | 0,0750 | 12,0000 |
| % de Var | 0,011 | 0,007 | 0,006 | 1,000 |
Esta análise foi realizada usando-se o método dos componentes principais e as configurações padrão (sem rotação). Os primeiros quatro fatores têm variância (autovalores) maior que 1. Os autovalores mudam menos marcadamente quando mais de 6 fatores são usados. Portanto, 4 fatores explicam a maior parte da variabilidade nos dados. Com base nesses resultados preliminares, repita a análise dos fatores e extraia somente 4 fatores, e experimente com diferentes rotações.
% Var
A porcentagem da variância (% Var) é a proporção da variabilidade nos dados explicada por cada fator. Os valores de % Var podem variar de 0 (0%) a 1 (100%).
Interpretação
Examine o valor % Var para cada fator. Os valores mais altos de % Var indicam que um fator explica mais da variabilidade. Portanto, você pode usar os valores % Var para determinar quais fatores são mais importantes.
O valor da comunalidade de % Var indica a variação total explicada por todos os fatores na análise. Use este valor para ajudar a determinar se o número de fatores usados na análise explica uma quantidade suficiente da variação total nos dados.
Cargas Fatoriais Não Rotacionadas e Itens Comuns
| Variável | Fator1 | Fator2 | Fator3 | Fator4 | Comum |
|---|---|---|---|---|---|
| Histórico Escolar | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Aparência | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Comunicação | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Adaptação à Empresa | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Experiência | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Adaptação ao Trabalho | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Carta | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Simpatia | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Organização | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potencial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Currículo | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Autoconfiança | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Variância | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % de Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
Nesses resultados, 0,303 ou 30,3% da variabilidade nos dados é explicado pelo Fator 1. Todos os quatro fatores juntos explicam 0,754 ou 75,4% ou a variabilidade nos dados.
Coeficientes de escores dos fatores
Os coeficientes de fatores estimam o peso relativo de cada variável no componente em uma análise de fatores. Quanto maior o valor absoluto do coeficiente, mais importante será a variável correspondente ao calcular o componente. O Minitab usa os coeficientes dos fatores para calcular os escores dos fatores, que são os valores estimados dos fatores. O Minitab calcula os escores dos fatores multiplicando os coeficientes dos escores dos fatores (listados em Fator 1, Fator 2 e assim por diante) pelos dados após eles terem sido escalados e centralizados subtraindo-se as médias.
Interpretação
- Examinar o comportamento das observações.
- Use em outra análise como regressão ou MANOVA.
Observação
Você deve padronizar as variáveis para usar os coeficientes estimados para calcular os escores dos fatores.
Gráfico scree
O gráfico scree exibe o número do fator versus seu autovalor correspondente. O gráfico scree ordena os autovalores do maior para o menor. Quando nenhuma rotação é feita, os autovalores da matriz de correlação se igualam às variâncias dos fatores.
Para exibir o gráfico scree, você deve clicar em Gráficos e selecionar o gráfico scree quando realizar a análise.
Interpretação
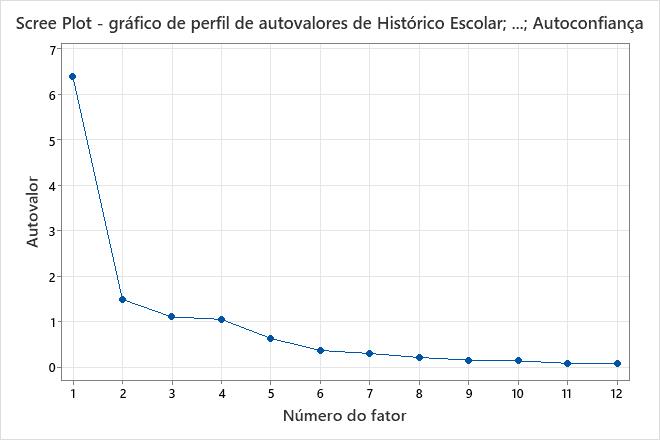
O gráfico scree mostra que os primeiros quatro fatores respondem pela maior parte da variabilidade total nos dados. (dados pelos autovalores). Os autovalores para os quatro primeiros fatores são todos maiores que 1. Os fatores restantes são responsáveis por uma proporção muito pequena da variabilidade e provavelmente não são importantes.
Gráfico de escores
O gráfico de escores representa os escores do segundo fator versus os escores do primeiro fator.
Para exibir o gráfico de escores, você deve clicar em Gráficos e selecionar o gráfico de escores quando realizar a análise.
Interpretação
Se os primeiros dois fatores forem responsáveis pela maior parte da variância nos dados, você pode usar o gráfico de escores para avaliar a estrutura de dados e detectar agrupamentos, outliers e tendências. Agrupamentos de dados no gráfico podem indicar duas ou mais distribuições separadas nos dados. Se os dados seguem uma distribuição normal e não houver nenhum outlier presente, os pontos são aleatoriamente distribuídos sobre o valor de 0.
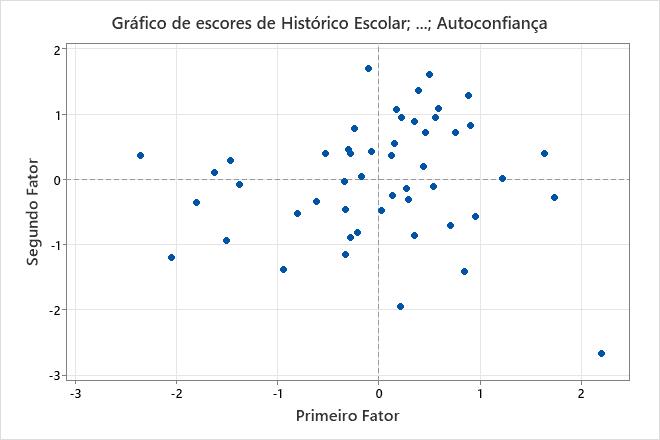
Neste gráfico de escores, os dados parecem normais e não há outliers extremos aparentes. Contudo, você pode querer investigar o valor dos dados no lado direito inferior do gráfico, que se localiza longe dos outros valores de dados.
Dica
Para ver o escore calculado de cada observação, mantenha o ponteiro sobre um ponto de dados no gráfico. Para criar gráficos de escores para outros fatores, armazene os escores e use .
Gráfico de cargas fatoriais
O gráfico de cargas fatoriais representa as cargas fatoriais rotacionadas de cada variável para o primeiro fator versus as cargas fatoriais rotacionadas para o segundo fator.
Para exibir o gráfico de cargas fatoriais, você deve clicar em Gráficos e selecionar o gráfico de cargas fatoriais quando realizar a análise.
Interpretação
Use o gráfico de cargas fatoriais para identificar quais variáveis têm o maior efeito nos fatores. As cargas fatoriais podem variar de -1 a 1. As cargas fatoriais próximas de -1 ou 1 indicam que a variável influencia fortemente o fator. As cargas fatoriais próximas de 0 indicam que a variável tem uma influência fraca no fator. Avaliar as cargas fatoriais também pode ajudá-lo a caracterizar cada fator em termos das variáveis. Depois de selecionar o número de fatores, tente diferentes rotações, de forma que você pode mais facilmente interpretar as cargas fatoriais do fator.
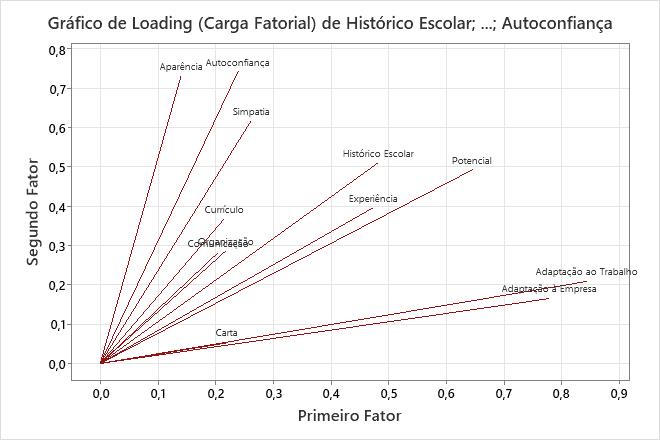
Para este gráfico de cargas fatoriais, foi realizada uma rotação varimax nos dados, o que torna os primeiros dois fatores mais fáceis de interpretar. Adequado para a função e Adequado para a empresa têm grandes cargas fatoriais positivas no fator 1, portanto, este fator descreve uma adequação do candidato para a posição. Aparência, Simpatia e Autoconfiança têm grandes cargas fatoriais positivas no fator 2, portanto, este fator descreve as qualidades pessoais de um candidato.
Biplot
O biplot sobrepõe o gráfico de escores e o gráfico de cargas fatoriais.
Para exibir o biplot, você deve clicar em Gráficos e selecionar o biplot quando realizar a análise.
Interpretação
Use o biplot para avaliar a estrutura dos dados e as cargas fatoriais dos primeiros dois fatores em um gráfico. O Minitab representa graficamente os escores do segundo fator versus os escores do primeiro fator, bem como as cargas fatoriais de ambos os fatores.
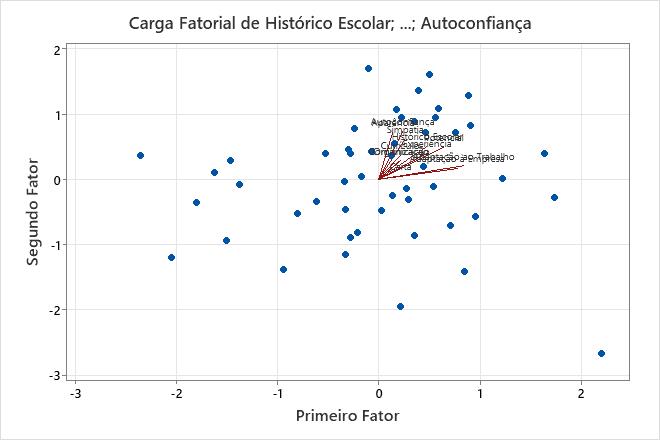
- Os dados parecem normais e nenhum outlier extremo está aparente. Contudo, você pode querer investigar o valor dos dados no lado direito inferior do gráfico, que se localiza longe dos outros valores de dados.
- Adequado para a função e Adequado para a empresa têm grandes cargas fatoriais positivas no fator 1, portanto, este fator descreve uma adequação do candidato para a posição.
- Aparência, Simpatia e Autoconfiança têm grandes cargas fatoriais positivas no fator 2, portanto, este fator descreve as qualidades pessoais de um candidato.
