Média
Na ligação por média, a distância entre dois agrupamentos é a distância média entre uma variável em um agrupamento e uma variável no outro agrupamento. A distância média é calculada com a seguinte matriz de distância:

Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
| Nk | número de variáveis no agrupamento k |
| Nl | número de variáveis no agrupamento l |
| Nm | número de variáveis no agrupamento m |
Centróide
Na ligação centróide, a distância entre dois agrupamentos é a distância entre os centróides ou médias dos agrupamentos. A distância é calculada com a seguinte matriz de distância:
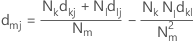
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
| Nk | número de variáveis no agrupamento k |
| Nl | número de variáveis no agrupamento l |
| Nm | número de variáveis no agrupamento m |
Completo
Com o método de ligação completo (também chamado método do vizinho mais distante), a distância entre dois agrupamentos é a distância máxima entre uma variável em um agrupamento e uma variável no outro agrupamento. A distância completa é calculada com a seguinte matriz de distância:
dmj = max (dkj, dlj)
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
McQuitty
Com o método de ligação de McQuitty, a distância é calculada com a seguinte matriz de distância:
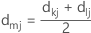
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos mi e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
Mediana
Na ligação por mediana, a distância entre dois agrupamentos é a distância mediana entre uma variável em um agrupamento e uma variável no outro agrupamento. A distância mediana é calculada com a seguinte matriz de distância:
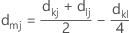
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
| dkl | distância entre os agrupamentos k e l |
Simples
Com o método de ligação simples (também chamado método do vizinho mais próximo), a distância entre dois agrupamentos é a distância mínima entre uma variável em um agrupamento e uma variável no outro agrupamento.
A distância é calculada com a seguinte matriz de distância:
dmj = min (dkj, dlj)
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
Ward
Na ligação de Ward, a distância entre dois agrupamentos é a soma dos desvios quadrados dos pontos aos centroides. O objetivo da ligação de Ward é minimizar a soma dos quadrados dentro do agrupamento. A distância é calculada com a seguinte matriz de distância:
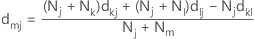
Observação
Na ligação de Ward, a distância entre dois agrupamentos pode ser maior do que d(max), o valor máximo na matriz da distância original, D. Se isso acontecer, a similaridade será negativa.
Notação
| Termo | Descrição |
|---|---|
| dmj | distância entre os agrupamentos m e j |
| m | agrupamento mesclado que consiste nos agrupamentos k e l, com m = (k,i) |
| dkj | distância entre os agrupamentos k e j |
| dlj | distância entre os agrupamentos l e j |
| dkl | distância entre os agrupamentos k e l |
| Nj | número de variáveis no agrupamento j |
| Nk | número de variáveis no agrupamento k |
| Nl | número de variáveis no agrupamento l |
| Nm | número de variáveis no agrupamento m |
