Um cientista social deseja estudar os efeitos do número de veículos de comunicação e de universidades e da taxa de alfabetização no ingresso da população em faculdades. Para 10 cidades do mundo, o cientista determina o número de cópias de jornais, rádios e aparelhos de TV por 1.000 pessoas. O cientista também registra a taxa de alfabetização e se há uma universidade em cada cidade. O cientista quer reduzir o número total de variáveis combinando variáveis com características semelhantes.
- Abra o conjunto de dados amostrais, MatrículasFaculdade.MWX.
- Selecione .
- Em Matriz de distância ou variáveis, insira JornalRádios 'Aparelhos de TV' 'Taxa de alfabetização' Universidade.
- Exemplo Método de ligação, selecione Média.
- Em Medida de distância, selecione Correlação.
- Selecione Exibir dendrograma.
- Clique em OK.
Interpretar os resultados
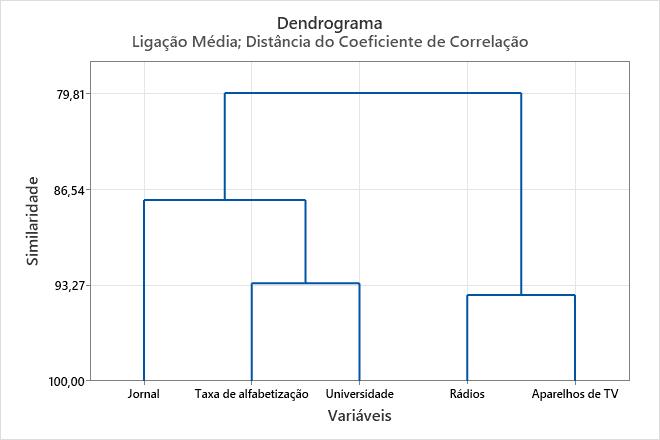
- O nível de similaridade diminui ligeiramente da etapa 1 (93,9666) para a etapa 2 (93,1548), depois diminui abruptamente na etapa 3 (87,3150), quando o número de agrupamentos muda de 3 para 2.
- A distância entre os agrupamentos unidos aumenta ligeiramente em aproximadamente 0,017 a partir da etapa até a etapa 2, depois aumenta mais abruptamente na etapa 3, quando o número de agrupamentos muda de 3 para 2.
A distância e os resultados de similaridade indicam que 3 agrupamentos são razoavelmente suficientes para a partição final. Se os cientistas sociais pensam que este agrupamento faz sentido intuitivo, ele é provavelmente uma boa escolha. O dendrograma exibe as informações na tabela na forma de um diagrama de árvore.
O cientista social deve realizar novamente a análise e especificar 3 agrupamentos na partição final. Quando você especifica uma partição final, o Minitab exibe tabelas adicionais que descrevem as características de cada agrupamento, incluído na partição final.
Passos de Amalgamação
| Passo | Número de agrupados | Nível de similaridade | Nível de distância | Agrupados reunidos | Novo agrupado | Número de obs. no novo agrupado | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93,9666 | 0,120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93,1548 | 0,136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87,3150 | 0,253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79,8113 | 0,403775 | 1 | 2 | 1 | 5 |