O que é experimento fatorial?
Um experimento fatorial é tipo de experimento planejado que permite observar os efeitos que vários fatores podem ter sobre uma resposta. Ao conduzir uma experiência, variando os níveis de todos os fatores, ao mesmo tempo, em vez de um de cada vez permite estudar as interações entre os fatores.
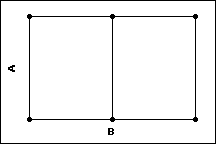
Experimento com dois fatores
- 2 níveis do fator A
- 3 níveis do fator B
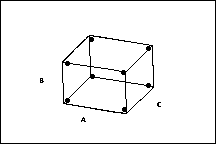
Experimento com três fatores
2 níveis de cada fator
Você pode executar o experimento fatorial completo ou uma fração do experimento fatorial.
Observação
Quando você tem um experimento fatorial com pontos centrais, pode testar se existe curvatura na superfície de resposta. No entanto, não é possível modelar o efeito daquela curvatura em nenhum outro lugar além do ponto central. Em outras palavras, só é possível calcular os valores ajustados nos pontos de extremidade e no ponto central do experimento e, portanto, não é possível criar um gráfico de contorno. É necessário ter termos quadráticos (por exemplo, termos ao quadrado) no modelo, a fim de modelar a curvatura em toda a superfície de resposta. Isso é possível com um experimento de superfície de resposta. Você pode ampliar o experimento fatorial com pontos axiais para criar um experimento de superfície de resposta central composto de um experimento fatorial.
O que é experimento fatorial completo e experimento fatorial fracionado?
Experimentos fatoriais completos
Um experimento fatorial completo é um experimento no qual pesquisadores medem respostas em todas as combinações dos níveis de fatores. O Minitab oferece dois tipos de experimentos fatoriais completos:
- Experimentos fatoriais completos com 2 níveis contendo apenas fatores de 2 níveis.
- experimentos fatoriais gerais completos que contêm fatores com mais de dois níveis.
O número de ensaios necessários para um experimento fatorial completo de 2 de níveis é 2k em que k é o número de fatores. Como o número de fatores em um experimento fatorial de 2 níveis aumenta, o número de ensaios necessário para fazer um experimento fatorial completo aumenta rapidamente. Por exemplo, um experimento fatorial completo de 2 níveis com 6 fatores requer 64 ensaios; um experimento com 9 fatores requer 512 ensaios. Uma meia-fração, o experimento fatorial fracionado exigiria apenas metade desses ensaios.
Experimentos fatoriais fracionados
Um experimento fracionado é aquele em que os experimentadores realizam apenas um subconjunto selecionado ou uma "fração" dos ensaios no experimento fatorial completo. Os experimentos fatoriais fracionados são uma boa opção quando os recursos são limitados ou o número de fatores no experimento é grande porque eles usam menos ensaios do que os experimentos fatoriais completos.
Um experimento fatorial fracionado utiliza um subconjunto de um experimento fatorial completo, de forma que alguns dos efeitos principais e interações de 2 fatores são confundidos e não podem ser separados dos efeitos de outras interações de ordem superior. Normalmente, os experimentadores estão dispostos a assumir que os efeitos de ordem superior são insignificantes a fim de obterem informações sobre os efeitos principais e as interações de ordem inferior com menos ensaios.
O que é experimento fatorial completo de 2 níveis?
Em um experimento fatorial completo de 2 níveis, cada fator experimental tem apenas dois níveis. Os ensaios experimentais incluem todas as combinações destes níveis de fator. Embora experimentos fatoriais de 2 de níveis sejam incapazes de explorar plenamente uma vasta região no espaço de fatores, eles fornecem informações úteis para uma quantidade de ensaios por fator relativamente pequena. Como experimentos fatoriais de 2 níveis podem identificar tendências importantes, é possível usá-los para fornecer orientação para a experimentação adicional. Por exemplo, quando você precisa explorar uma região onde acredita que possam existir definições ótimas, é possível ampliar um experimento fatorial para formar um experimento central composto.
Comparação
Os diagramas a seguir mostram um experimento fatorial completo comparado a um ½ experimento fatorial fracionado.
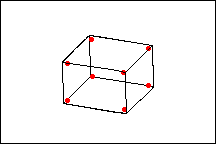
Experimento fatorial completo
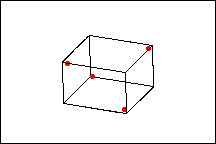
½ experimento fatorial fracionado
O experimento fatorial completo contém duas vezes mais pontos do que o ½ experimento fracionário. A resposta só é medida em quatro dos oito pontos de vértice possíveis da parte fatorial do experimento. No entanto, com este experimento, os efeitos principais serão confundidos com as de interações de 2 fatores.
Como o Minitab ordena as frações de um experimento
| Fração | Ordem Padrão (Yates) | Gerador de planejamento |
|---|---|---|
| 1 | – – – | D = –AB, E = –AC, F = –BC |
| 2 | + – – | D = +AB, E = –AC, F = –BC |
| 3 | – + – | D = –AB, E = +AC, F = –BC |
| 4 | + + – | D = +AB, E = +AC, F = –BC |
| 5 | – – + | D = –AB, E = –AC, F = +BC |
| 6 | + – + | D = +AB, E = –AC, F = +BC |
| 7 | – + + | D = –AB, E = +AC, F = +BC |
| 8 | + + + | D = +AB, E = +AC, F = +BC |
A fração principal é sempre a última, a única que tem todos os sinais +.
| Ensaio | A | B | C | D = AB | E = –AC | F = –BC |
|---|---|---|---|---|---|---|
| 1 | – | – | – | + | – | – |
| 2 | + | – | – | – | + | – |
| 3 | – | + | – | – | – | + |
| 4 | + | + | – | + | + | + |
| 5 | – | – | + | + | + | + |
| 6 | + | – | + | – | – | + |
| 7 | – | + | + | – | + | – |
| 8 | + | + | + | + | – | – |
Como escolher uma fração diferente do padrão
Ao criar um experimento fatorial fracionado, o Minitab utiliza a fração principal por padrão. A fração principal é a fração em que todos os sinais são positivos. No entanto, pode haver situações em que um experimento contém pontos que apresentam impraticabilidade na execução e a escolha de uma fração apropriada pode evitar tais pontos.
- D = –AB E = –AC
- D = AB E = –AC
- D = –AB E = AC
- D = AB E = AC
Por exemplo, suponha que você não possa entrar executar seu experimento com todos os cinco fatores estabelecidos pelo seu alto nível. A fração principal contém este ponto, mas a terceira fração não.
