Matriz de experimento
Primeiro, o Minitab cria uma matriz de experimento a partir dos fatores e do modelo que você especificar. As colunas desta matriz representam os termos no modelo. Em seguida, o Minitab adiciona mais colunas ao termo constante, blocos e termos de ordem superior para completar a matriz de experimento para o modelo na análise.
Experimentos com todos os fatores contínuos
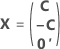
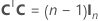
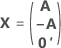
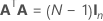
A matriz de experimento completa contém colunas além das colunas que representam fatores. A matriz de experimento contém uma coluna de 1s para o termo constante. A matriz de experimento completa também inclui colunas que representam os termos quadrados ou de interação no modelo.
Experimentos com fatores categóricos
Para um experimento que inclui fatores categóricos, o Minitab substitui a linha do ponto central único na matriz de experimento por 2 pseudopontos centrais. Se o experimento tiver apenas 1 fator categórico, existem apenas dois pseudopontos centrais possíveis, de forma que ambos os pontos estejam no experimento.
No caso em que o experimento tem mais de 2 fatores categóricos, o Minitab usa um algoritmo iterativo para selecionar 2 pseudopontos centrais a serem incluídos. O algoritmo procura minimizar variância dos coeficientes de regressão dos efeitos lineares no modelo.
Notação
| Termo | Descrição |
|---|---|
| C | Uma matriz de conferência |
| 0' | Uma linha de zeros em uma matriz que representa um ponto central em um ensaio |
| In | a matriz de identidade n × n |
| A | Uma matriz que é um subconjunto de uma matriz com conferência com N linhas e n colunas em que  |
| N | O número de linhas no subconjunto das colunas da matriz de conferência |
| n | O número de fatores em um experimento |
Coeficiente (Coef)
Nos termos da matriz, a fórmula que calcula o vetor dos coeficientes do modelo é:

Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| Y | vetor de resposta |
Transformação Box-Cox
A transformação de Box-Cox seleciona valores de lambda, conforme mostrado a seguir, que minimizam a soma dos quadrados dos resíduos. A transformação resultante é Y λ quando λ ≠ 0 e ln(Y) quando λ = 0. Quando λ < 0, o Minitab também multiplica a resposta transformada por -1 para manter a ordem da resposta não transformada.
O Minitab pesquisa um valor ideal entre −2 e 2. Os valores que estão fora desse intervalo podem não resultar em um ajuste melhor.
A seguir estão algumas transformações comuns onde Y é a transformação dos dados Y:
| Valor lambda (λ) | Transformação |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 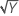 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Regressão ponderada
A regressão de mínimos quadrados ponderada é um método para lidar com as observações que têm variâncias não constantes. Se as variâncias são não constantes, observações com:
- grandes variâncias devem ser dadas em relação a pesos pequenos
- pequenas variâncias devem ser dadas em relação a pesos grandes
A escolha comum de pesos é o inverso da variância do erro puro na resposta.
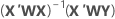
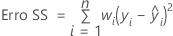
Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| X' | transposição da matriz do experimento |
| W | uma matriz n x n com os pesos na diagonal |
| Y | vetor de valores de resposta |
| n | número de observações |
| wi | peso para a ia observação |
| yi | valor da resposta para a ia observação |
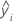 | valor ajustado para a ia observação |
