Neste tópico
Gráficos de probabilidade normal de resíduos
Um gráfico de probabilidade normal dos resíduos mostra os resíduos versus seus valores esperados quando a distribuição é normal.
Interpretação
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
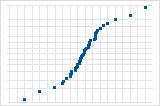
A curva S sugere uma distribuição com caudas longas.
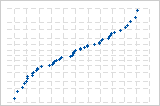
A curva S invertida sugere uma distribuição com caudas curtas.
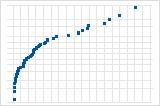
A curva descendente implica uma distribuição assimétrica à direita.
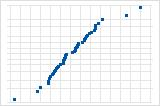
Alguns pontos situados longe da linha sugerem uma distribuição com outliers.
Se você vir um padrão não-normal, use os outros gráficos de resíduos para verificar outros problemas com o modelo, como termos faltantes ou um efeito de ordem de tempo. Se os resíduos não seguirem uma distribuição normal, os intervalos de confiança e os valores-p podem ser inexatos.
Resíduos versus valores ajustados
O gráfico de resíduos versus ajustes representa graficamente os resíduos no eixo Y e os valores ajustados no eixo X.
Interpretação
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |

Gráfico com outlier
Um dos pontos é muito maior do que todos os outros pontos. Portanto, a questão é um outlier. Se houver muitos outliers, o modelo pode não ser aceitável. Você deve tentar identificar a causa de todos os outliers. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
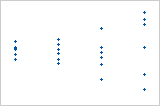
Gráfico com variância não constante
A variância dos resíduos aumenta com os valores ajustados. Observe que, como o valor dos ajustes aumenta, a dispersão entre os resíduos se torna mais ampla. Este padrão indica que as variâncias dos resíduos são desiguais (não constante).
| Problema | Solução possível |
|---|---|
| Variância não constante | Considere usar uma transformação de Box-Cox da variável resposta ou pesos.. |
| Um outlier ou um ponto influente |
|
Resíduos x ordem
O gráfico de resíduos versus ordem mostra os resíduos na ordem em que os dados foram coletados.
Interpretação
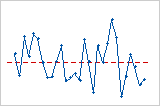
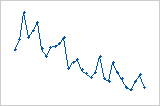
Tendência
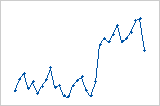
Turno
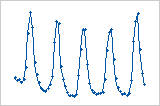
Ciclo
Resíduos versus variáveis
O gráfico de resíduos versus variáveis apresenta os resíduos comparados com outras variáveis. A variável já pode estar incluída em seu modelo. Ou, a variável pode não estar no modelo, mas você suspeita que afeta a resposta.
Interpretação
Se você observar um padrão não aleatória nos resíduos, isso indica que a variável afeta a resposta de uma forma sistemática. Considere a inclusão desta variável em uma análise.
