Métodos em Análise de resposta binária para filtragem de experimentos definitiva

A extensão dos modelos lineares clássicos para modelos lineares generalizados tem duas partes: uma distribuição da família exponencial e uma função de ligação.

A família exponencial

A primeira parte estende o modelo linear às variáveis de resposta que são membros de uma grande família de distribuições chamada a família exponencial. Os membros da família exponencial de distribuições têm funções de distribuição de probabilidade para uma resposta observada nesta forma geral:

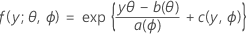
onde a(∙), b(∙) e c(∙) dependem da distribuição da variável de resposta. O parâmetro θ é um parâmetro de localização é frequentemente chamado de parâmetro canônico, e ϕ é chamado de parâmetro de dispersão. A função a(ϕ) é normalmente da forma a(ϕ)= ϕ/ ω, onde ω é uma constante conhecida ou peso que pode variar de uma observação para outra. (No Minitab, quando os pesos recebem a função a(ϕ), eles são ajustados de forma correspondente.)

Membros da família exponencial podem ser distribuições discretas ou distribuições contínuas. Exemplos de distribuições contínuas que são membros da família exponencial são as distribuições normal e gama. Exemplos de distribuições discretas que são membros da família exponencial são distribuições binomiais e a Poisson. A tabela a seguir dá as características de algumas dessas distribuições.

Distribuição	ϕ	b(θ)	a(φ)	c(y, ϕ)
Normal	σ2	θ2/2	φω
Binomial	1		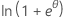φ/ω	-ln(y!)
Poisson	1	exp(θ)	φ/ω

A função de ligação

A segunda parte é a função de ligação. A função de ligação relaciona a média da resposta na i^ésima observação para uma preditora linear desta forma:

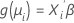
O modelo linear clássico é um caso especial desta fórmula geral onde a função de ligação é a função de identidade.

A escolha da função de ligação na segunda parte depende da distribuição específica da família exponencial da primeira parte. Em particular, cada distribuição na família exponencial tem uma função de ligação especial chamada de função de ligação canônica. Esta função de ligação satisfaz à equação g (μ_i) = X_i'β = θ, onde θ é o parâmetro canônico. A função de ligação canônica resulta em algumas propriedades estatísticas desejáveis do modelo. As estatísticas de qualidade do ajuste podem ser usadas para comparar ajustes usando-se diferentes funções de ligação. Determinadas funções de ligação podem ser usadas por motivos históricos ou porque elas têm um significado especial em uma disciplina. Por exemplo, uma vantagem da função de ligação logit é que ela fornece uma estimativa das razões de chances. Outro exemplo é que a função de ligação normit supõe que exista uma variável subjacente que segue uma distribuição normal que é classificada em categorias binárias.

O Minitab oferece três funções de ligação. As diferentes funções de ligação possibilitam encontrar modelos que se ajustem adequadamente a uma grande variedade de dados. As funções de ligação são logit, normit (também chamado de probit) e gompit (também chamado de complemento log-log). Elas são o inverso da função de distribuição logística acumulada padrão (logit), o inverso da função de distribuição normal acumulada padrão (normit) e o inverso da função de distribuição de Gompertz (gompit). O logit é a função de ligação canônica para modelos binomiais e, por consequência, o logit é a função de ligação padrão.

Modelo	Nome	Função de ligação, g(μi)
Binomial	logito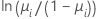
Binomial	normit (probit)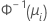
Binomial	gompit (complemento log-log)

Notação

Termo	Descrição
μi	a resposta média da iésima linha
g(μi)	a função de ligação
X	o vetor das variáveis preditoras
β	o vetor dos coeficientes associados às preditoras
	a função de distribuição acumulada inversa da distribuição normal

Descreve um conjunto único de valores de fator/covariável em um conjunto de dados. O Minitab calcula probabilidades de evento, resíduos e outras medidas diagnósticas para cada padrão de fator/covariável.

Por exemplo, se um conjunto de dados inclui os fatores sexo e raça e a covariável idade, a combinação dessas preditoras pode conter tantos padrões de covariáveis diferentes quanto de indivíduos. Se um conjunto de dados só inclui os fatores raça e sexo, cada um codificado em dois níveis, só há quatro padrões de fator/covariáveis possíveis. Se você inserir seus dados como frequências, ou como sucessos, tentativas ou falhas, cada linha conterá um padrão de fator/covariável.

Primeiro, o Minitab cria uma matriz de experimento a partir dos fatores e do modelo que você especificar. As colunas desta matriz representam os termos no modelo. Em seguida, o Minitab adiciona mais colunas ao termo constante, blocos e termos de ordem superior para completar a matriz de experimento para o modelo na análise.

Experimentos com todos os fatores contínuos

A forma da matriz do experimento depende da existência de uma matriz de conferência com o mesmo número de linhas como fatores. Quando este critério é verdadeiro, as colunas da matriz de experimento que representam os fatores têm esta forma:

Em que C é uma matriz de conferência n× n com elementos {-1, 0, 1} que satisfaz esta propriedade:

Quando não existe uma matriz de conferências do tamanho correto, as colunas que representam os fatores são um subconjunto de uma matriz de conferência maior:

Em que A é uma matriz N× n com elementos {-1, 0, 1} que satisfaz esta propriedade:

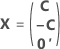
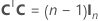
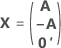
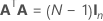
A matriz de experimento completa contém colunas além das colunas que representam fatores. A matriz de experimento contém uma coluna de 1s para o termo constante. A matriz de experimento completa também inclui colunas que representam os termos quadrados ou de interação no modelo.

Experimentos com fatores categóricos

Para um experimento que inclui fatores categóricos, o Minitab substitui a linha do ponto central único na matriz de experimento por 2 pseudopontos centrais. Se o experimento tiver apenas 1 fator categórico, existem apenas dois pseudopontos centrais possíveis, de forma que ambos os pontos estejam no experimento.

No caso em que o experimento tem mais de 2 fatores categóricos, o Minitab usa um algoritmo iterativo para selecionar 2 pseudopontos centrais a serem incluídos. O algoritmo procura minimizar variância dos coeficientes de regressão dos efeitos lineares no modelo.

Notação

Termo	Descrição
C	Uma matriz de conferência
0'	Uma linha de zeros em uma matriz que representa um ponto central em um ensaio
In	a matriz de identidade n × n
A	Uma matriz que é um subconjunto de uma matriz com conferência com N linhas e n colunas em que
N	O número de linhas no subconjunto das colunas da matriz de conferência
n	O número de fatores em um experimento