Matriz de experimento
O Minitab gera uma matriz de experimento para cada experimento. A primeira coluna é uma coluna de um para o termo constante. Se o experimento foi disposto em k blocos, existem (k - 1) colunas de blocos. O Minitab usa o mesmo método de blocos de codificação que os Modelos Fatoriais. Isto é seguido por uma coluna para cada efeito principal. Os termos com fatores categóricos podem ter mais de uma coluna. Se o modelo tiver termos ao quadrado, há uma coluna para cada termo ao quadrado. A coluna para um termo ao quadrado é o produto do fator correspondente consigo mesmo. Se o modelo tem termos de interação, então há uma coluna para cada termo de interação. As interações que incluem fatores categóricos podem ter mais do que uma coluna. A coluna para um termo de interação é o produto das duas colunas que são cruzadas.
Se o Minitab remover alguns termos porque os dados não podem sustentá-los, estes termos não estão na matriz do experimento armazenado. As colunas armazenadas coincidem com os coeficientes que são exibidos.
Coeficiente (Coef)
Nos termos da matriz, a fórmula que calcula o vetor dos coeficientes do modelo é:

Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| Y | vetor de resposta |
Transformação Box-Cox
A transformação de Box-Cox seleciona valores de lambda, conforme mostrado a seguir, que minimizam a soma dos quadrados dos resíduos. A transformação resultante é Y λ quando λ ≠ 0 e ln(Y) quando λ = 0. Quando λ < 0, o Minitab também multiplica a resposta transformada por -1 para manter a ordem da resposta não transformada.
O Minitab pesquisa um valor ideal entre −2 e 2. Os valores que estão fora desse intervalo podem não resultar em um ajuste melhor.
A seguir estão algumas transformações comuns onde Y é a transformação dos dados Y:
| Valor lambda (λ) | Transformação |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 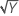 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
