Neste tópico
Desviância

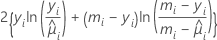
Os graus de liberdade do teste dependem do tamanho da amostra e do número de termos do modelo:

Notação
| Termo | Descrição |
|---|---|
| Lf | a log-verossimilhança do modelo completo |
| Lc | a log-verossimilhança do modelo com um subconjunto de termos do modelo completo |
| yi | o número de evento da iésima linha nos dados |
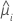 | a resposta média estimada da iésima linha nos dados |
| mi | o número de ensaios da iésima linha dos dados |
| n | o número de linhas nos dados |
| p | os graus de liberdade da regressão |
Pearson
A estatística qui-quadrado de Pearson generalizada avalia a diferença relativa entre os valores observados e ajustados.
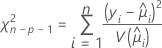
Os graus de liberdade do teste dependem do tamanho da amostra e do número de termos do modelo. A estatística de Pearson tem uma distribuição de qui-quadrado exata para dados normais. Para dados não normais, como a distribuição binomial e a distribuição de Poisson, a estatística se aproxima assintoticamente da distribuição.
Notação
| Termo | Descrição |
|---|---|
| n | o número de linhas nos dados |
| p | os graus de liberdade da regressão |
| yi | o valor da resposta do iésimo padrão fator/covariável |
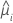 | a resposta média estimada da iésima linha |
| V(·) | a função de variância do modelo, definido a seguir |
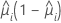
Hosmer-Lemeshow
A fórmula é:
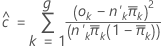
Para formar os grupos, o Minitab ordena as probabilidades estimadas e depois tenta criar 10 grupos de igual tamanho.
O número esperado de eventos em um grupo é:
eventos esperados = 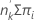
O valor esperado para o número de não eventos é:
não eventos esperados = 
Notação
| Termo | Descrição |
|---|---|
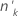 | O número de ensaios no késimo grupo |
| ok | O número de eventos entre o 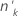 padrões de fator/covariável padrões de fator/covariável |
 | A probabilidade estimada média de cada grupo |
| πi | As probabilidades ajustadas para os padrões de fator/covariável em um grupo |
