Neste tópico
Valores ajustados e preditos
Para calcular a predição, inverta a função de ligação do modelo. As funções inversas estão nesta tabela.
| Função de ligação | Fórmula para predição |
|---|---|
| Logit | 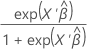 |
| Normit | 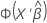 |
| Gompit |  |
Notação
| Termo | Descrição |
|---|---|
| exp(·) | a função exponencial |
| Φ(·) | a função de distribuição cumulativa da distribuição normal |
| X' | a transposição do vetor dos pontos para predizer |
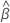 | o vetor de coeficientes estimados |
Erro padrão de valores ajustados e predições
Em geral, o erro padrão do ajuste tem a seguinte forma:
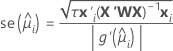
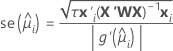
As seguintes fórmulas dão o erro padrão do ajuste para diferentes funções de link:
- Logito
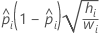
- Normito
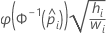
- Gompito

Observe a seguinte relação que se aplica às fórmulas da tabela: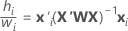
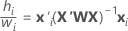
Onde 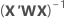 é a partir dos dados de treinamento somente quando há um conjunto de dados de teste para validação.
é a partir dos dados de treinamento somente quando há um conjunto de dados de teste para validação.
Notação
| Termo | Descrição |
|---|---|
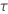 | 1, for the binomial and Poisson models |
| xi | the vector of a design point |
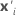 | the transpose of xi |
| X | the design matrix |
| W | the weight matrix |
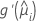 | the first derivative of the link function evaluated at 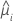 |
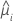 | the predicted mean response |
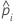 | the predicted probability for the design point in a binary logistic model |
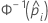 | the inverse cumulative distribution function of the standard normal distribution for the predicted probability in a binary logistic model |
 | the probability density function of the standard normal distribution |
Limites de confiança para ajustes e predições
Os limites de confiança usam o método de aproximação Wald. Esta é a fórmula para um 100 (1 − α)% intervalo de confiança bilateral:
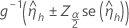
Notação
| Termo | Descrição |
|---|---|
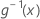 | o inverso da função de ligação avaliado em x |
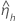 | 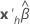 |
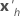 | a transposição do vetor das preditoras |
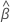 | o vetor de coeficientes estimados |
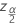 | o valor da função de distribuição acumulada inversa da distribuição normal avaliada em  |
| α | o nível de significância |
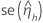 |  |
| X | a matriz de experimento |
| W | a matriz de peso |
 | 1, para modelos binomiais |
