Neste tópico
Resíduos de Pearson
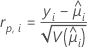
Elementos do qui-quadrado de Pearson que podem ser usados para detectar padrões de fator/covariável mal ajustados. O Minitab armazena o resíduo de Pearson para o iésimo padrão de fator/covariável. A fórmula é:
Notação
| Termo | Descrição |
|---|---|
| yi | o valor da resposta do iésimo padrão de fator/covariável |
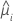 | o valor ajustado do iésimo padrão de fator/covariável |
| V | a função de variância do modelo em 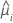 |
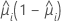
Resíduos de Pearson padronizados e deletados
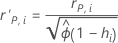
Notação
| Termo | Descrição |
|---|---|
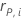 | o resíduo de Pearson para o iésimo padrão de fator/covariável |
 | 1, para modelos binomiais |
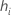 | o leverage do iésimo padrão de fator/covariável |
Resíduos deviance
Os resíduos deviance estão baseados na deviance modelo e são úteis na identificação de padrões de fatores/covariáveis mal ajustados. A deviance do modelo é uma estatísticas de qualidade do ajuste que está baseada na função de log-verossimilhança. Os resíduos deviance definidos para o iésimo padrão de fatores/covariáveis é:

Notação
| Termo | Descrição |
|---|---|
| yi | o valor da resposta do iésimo padrão de fatores/covariáveis |
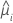 | o valor ajustado do iésimo padrão de fatores/covariáveis |
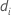 | a deviance para o iésimo padrão de fatores/covariáveis |
Resíduo deviance padronizado

Notação
| Termo | Descrição |
|---|---|
| rD,i | O resíduo de deviance para o iésimo padrão de fatores/covariáveis |
| hi | O leverage do iésimo padrão de fatores/covariáveis |
Resíduo deviance deletado

Notação
| Termo | Descrição |
|---|---|
| yi | o valor da resposta do iésimo padrão fator/covariável |
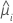 | o valor ajustado do iésimo padrão de fator ou covariável |
| hi | o leverage do iésimo padrão de fator/covariável |
| r'D,i | o resíduo de deviance padronizado para o iésimo padrão de fator/covariável |
| r'P,i | o resíduo de Pearson padronizado para o iésimo padrão de fator/covariável |
1. Pregibon, D. (1981). "Diagnósticos de regressão logística". The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.
Delta qui-quadrado
O Minitab calcula a mudança no qui-quadrado de Pearson devido à deleção de todas as observações com o jésimo padrão de fator/covariável. O Minitab armazena um valor de delta qui-quadrado para cada padrão de fator/covariável distinto nos dados. Você também pode usar o qui-quadrado delta para detectar padrões de fatores/covariáveis mal ajustados. A fórmula para o delta qui-quadrado é:
Fórmula
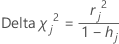
Notação
| Termo | Descrição |
|---|---|
| hj | leverage |
| rj | Resíduos de Pearson |
Delta deviance
O Minitab calcula a mudança na estatística deviance deletando todas as observações com o jésimo padrão de fator/covariável. O Minitab armazena um valor para cada padrão de fator/covariável distinto nos dados. Você pode usar o deviance delta para detectar padrões de fatores/covariáveis mal ajustados. A mudança na estatística deviance é:
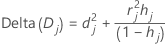
Notação
| Termo | Descrição |
|---|---|
| hj | leverage |
| rj | Resíduos de Pearson |
| dj | resíduos deviance |
Delta beta (padronizado)
O Minitab calcula a mudança deletando todas as observações com o jésimo padrão de fator/covariável. Um valor é armazenado para cada padrão de fator/covariável distinto nos dados. Você pode usar o delta padronizado β para detectar padrões de fatores/covariáveis que têm uma forte influência nas estimativas dos coeficientes. Este valor está baseado no resíduo de Pearson padronizado.
Fórmula
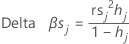
Notação
| Termo | Descrição |
|---|---|
| hj | leverage |
| rs j | resíduos de Pearson padronizados |
Delta beta
O Minitab calcula a mudança deletando todas as observações com o jésimo padrão de fator/covariável. Um valor é armazenado para cada padrão de fator/covariável distinto nos dados. Você pode usar o delta β para detectar padrões de fatores/covariáveis que têm uma forte influência nas estimativas dos coeficientes. Este valor está baseado no resíduo de Pearson.
Fórmula
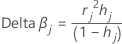
Notação
| Termo | Descrição |
|---|---|
| hj | leverage |
| rj | Resíduos de Pearson |
Leverages
Os leverages são elementos diagonais da matriz de chapéu generalizada. Os leverages são úteis na detecção de padrões de fatores/covariáveis que podem ter uma influência significativa nos resultados.
Fórmula
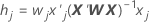
Notação
| Termo | Descrição |
|---|---|
| wj | o jésimo elemento diagonal da matriz ponderada a partir dos ajustes dos coeficientes |
| xj | a jésima linha da matriz de planejamento |
| X | a matriz de planejamento |
| X' | a transposição do x |
| W | a matriz ponderada da estimativa dos coeficientes |
Distância de Cook
Fórmula
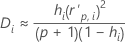
Notação
| Termo | Descrição |
|---|---|
| hi | o leverage do iésimo padrão de fator/covariável |
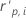 | o resíduo de Pearson padronizado para o iésimo padrão de fator/covariável |
| p | os graus de liberdade da regressão |
DFITS
Uma medida da influência de uma deleção única nos valores ajustados. As observações com grandes valores DFITS podem ser outliers. O Minitab calcula um valor aproximado para DFITS.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| hi | O leverage do ponto de dados |
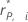 | O residual de Pearson deletado do ponto de dados |
Fator de inflação de variância (VIF)

Notação
| Termo | Descrição |
|---|---|
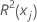 | coeficiente de determinação com xj como a variável de resposta e os outros termos no modelo como as preditores |
1. P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2a Edição, Chapman & Hall/CRC, Londres.
