Neste tópico
Experimentos simplex-centróides
Um experimento simplex-centróide para uma mistura com q componentes consiste em 2**q - 1 pontos. Os pontos do experimento são da seguinte maneira:
- Todos os pontos (x1, x2, ..., xq) em que um componente, xi = 1, e o resto são igual a 0. Estes são chamados de pontos de vértice.
- Todos os pontos onde um componente, xi = 1/2, outro componente, xj = 1/2, e o resto são igual a 0.
- Todos os pontos onde um componente, xi = 1/3, outro componente, xj = 1/3, outro componente, xk = 1/3, e o resto são igual a 0.
- Este padrão continua até que todos os componentes sejam 1/q. Este último ponto (em que todos os componentes são iguais) é chamado de centro ou centróide do experimento.
Experimentos simplex-lattice
| Grau de lattice (m) | Número de componentes (q) |
|---|---|
| 1 | 2 a 20 |
| 2 | 2 a 20 |
| 3 | 2 a 17 |
| 4 | 2 a 11 |
| 5 | 2 a 8 |
| 6 | 2 a 7 |
| 7 | 2 a 6 |
| 8 | 2 a 5 |
| 9 | 2 a 5 |
| 10 | 2 a 5 |
Experimentos com vértices extremos
O Minitab gera os vértices extremos do espaço de experimento restrito usando o algoritmo XVERT e, em seguida, calcula os pontos centróides até o grau especificado usando o algoritmo CONAEV de Piepel. Consulte Cornell1 e St. John2 para obter mais informações.
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
- R.C. St. John (1984). "Experiments With Mixtures in Conditioning and Ridge Regression," Journal of Quality Technology 16, pp.81-96.
Tipos de experimento
O Minitab permite a análise de dados de três tipos de experimentos:
| Tipo | A resposta depende de... |
| Mistura | as proporções relativas apenas dos componentes. |
| Variáveis de processo de mistura | os componentes e as variáveis do processo. As variáveis de processo são fatores em um experimento que não fazem parte da mistura, mas podem afetar a resposta. |
| Quantidades de mistura | as proporções relativas dos componentes e a quantidade total da mistura. |
Colocar pontos axiais em experimentos aumentados
O Minitab aumenta (ou adiciona pontos) o experimento como mostrado abaixo. Cada ponto é adicionado a meio caminho entre um vértice e o centro do experimento.
Ao aumentar um experimento, é possível obter informações sobre as respostas no interior do experimento, em vez de simplesmente depender dos pontos nas bordas.
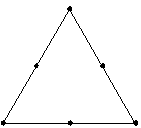
Não aumentado
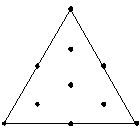
Aumentado
Conversão de unidades de componente
No Minitab é possível criar experimentos e analisar os dados em termos de quantidade, unidades, proporção e pseudocomponentes.
Para converter dados de valor para unidades de proporção, a fórmula é:
- Proporção = Quantidade / Total
Se o total = 1, as unidades de proporção = unidades de quantidade.
Para converter a proporção para unidades de pseudocomponentes, a fórmula é:
- Pseudo = (proporção - baixa) / (1 - soma dos limites inferiores)
- Proporção = pseudo * (1 - soma dos limites inferiores) + limite inferior
Se todos os limites inferiores = 0, então as unidades pseudo = unidades de proporção
Termos do modelo
Os experimentos de mistura incluem muitos tipos de termos de modelo. Os termos e as suas representações são:
| Modelo | Termos |
| Linear | A B C |
| Quadrático | Linear + AB AC BC |
| Cúbico especial | Quadrático + ABC |
| Cúbico completo | Cúbico especial + AB(A-B) AC(A-C) BC(B-C) |
| Quártico especial | Quadrático + AABC ABBC ABCC |
| Quártico completo | Quártico especial + AB(A-B) AC(A-C) BC(B-C) AB(A-B)2 AC(A-C)2 BC(B-C)2 |
Observe que não há nenhum termo constante em modelos de mistura. Os termos inversos incluem 1/A, 1/B, 1/C, etc.
