Neste tópico
Coeficiente (Coef)
O Minitab usa a estimativa dos mínimos quadrados para calcular os coeficientes.
Em termos matriciais, as estimativas dos mínimos quadrados dos coeficientes são:
b = (X'X)-1X'y
Para obter mais informações sobre os coeficientes de modelos de ordem superior, consulte Cornell1.
Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| y | coluna de resposta |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
Erro padrão do coeficiente (Coef. SE)
Para regressão linear simples, o erro padrão do coeficiente é:
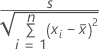
Os erros padrão dos coeficientes para regressão múltipla são as raízes quadradas dos elementos diagonais desta matriz:
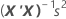
Notação
| Termo | Descrição |
|---|---|
| xi | iésimo valor da preditora |
 | média da preditora |
| X | matriz de experimento |
| X' | transposição da matriz de experimento |
| s2 | quadrado médio do erro |
Valor de T
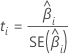
Notação
| Termo | Descrição |
|---|---|
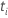 | estatística de teste para o  coeficiente coeficiente |
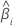 |  coeficiente estimado coeficiente estimado |
 | erro padrão de  coeficiente estimado coeficiente estimado |
Valor-p – Tabela Coeficientes
O valor-p bilateral para hipótese nula que um coeficiente de regressão igual a 0 é:
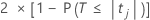
Os graus de liberdade são os graus de liberdade para erro, da seguinte forma:
n – p
Notação
| Termo | Descrição |
|---|---|
 | A função distribuição acumulada da distribuição t com graus de liberdade iguais aos graus de liberdade para o erro. |
| tj | A estatística t para o jésimo coeficiente. |
| n | O número de observações no conjunto de dados. |
| p | A soma dos graus de liberdade para os termos. |
Fator de inflação de variância (VIF)
O VIF pode ser obtido pela regressão de cada preditor sobre os preditores restantes e observando-se o valor de R2.
Fórmula
Para a preditora xj, o VIF é:

Notação
| Termo | Descrição |
|---|---|
| R2( xj) | coeficiente de determinação com xj como a variável de resposta e os outros termos no modelo como as preditoras |
