Neste tópico
Soma de quadrados (SS)
Nos termos da matriz, estas são as fórmulas para as diferentes somas dos quadrados:

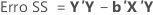

O Minitab decompõe o componente Tratamentos SS ou Regressão SS na quantidade de variação explicada por cada termo usando tanto a soma sequencial de quadrados como a soma ajustada de quadrados.
Notação
| Termo | Descrição |
|---|---|
| b | vetor de coeficientes |
| X | matriz do experimento |
| Y | vetor de valores de resposta |
| n | número de observações |
| J | n por n matriz de 1s |
Soma dos quadrados sequencial
O Minitab decompõe a o componente de Regressão SS ou Tratamentos da variância em somas dos quadrados sequenciais para cada fator. As somas dos quadrados sequenciais dependem da ordem dos fatores preditores e são inseridas no modelo. A soma dos quadrados sequencial é a parte única da Regressão SS explicada por um fator, considerando-se todos os fatores inseridos anteriormente.
Por exemplo, se você tem um modelo com três fatores ou preditores, X1, X2 e X3, a soma dos quadrados sequencial para X2 mostra quanto da variação restante é explicada por X2, considerando-se que X1 já está no modelo. Para obter uma sequência de fatores diferente, repita a análise e insira os elementos em uma ordem diferente.
Soma dos quadrados ajustada
A soma dos quadrados ajustada não depende da ordem em que os termos são inseridos no modelo. A soma dos quadrados ajustada é a quantidade de variação explicada por um termo, tendo em conta todos os outros termos no modelo, independentemente da ordem em que os termos entram no modelo.
Por exemplo, se você tem um modelo com três fatores, X1, X2 e X3, a soma ajustada dos quadrados para X2 mostra quanto da variação restante do termo para X2 é explicada, considerando-se que os termos para X1 e X3 já estão no modelo.
Os cálculos para as somas dos quadrados ajustado para três fatores são:
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) ou
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
em que SSR(X3 | X1, X2) é a soma dos quadrados ajustada para X3, dado que X1 e X2 estão no modelo.
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) ou
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
em que SSR(X2, X3 | X1) é a soma dos quadrados ajustados para X2 e X3, dado que X1 está no modelo.
Você pode estender estas fórmulas se tiver mais de 3 fatores em seu modelo1.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Graus de liberdade (DF)
Indica o número de informações independentes que envolvem os dados de resposta necessários para calcular as somas dos quadrados. Os graus de liberdade para cada componente do modelo são:
| Regressão DF | = p - 1 |
| Erro DF | = n - p |
| Total | = n - 1 |
em que n = número de observações e p = número de termos no modelo.
MS Ajust – Regressão
A fórmula para o Quadrado Médio (MS) da regressão é:

Notação
| Termo | Descrição |
|---|---|
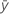 | resposta média |
 | ia resposta ajustada |
| p | o número de termos no modelo |
QM aj. – Erro
O quadrado médio do erro (também abreviado como MS Erro ou MSE e denotado como s2) é a variação em torno da linha de regressão ajustada. A fórmula é:

Notação
| Termo | Descrição |
|---|---|
| yi | io valor de resposta observada |
 | ia resposta ajustada |
| n | número de observações |
| p | número de coeficientes no modelo |
F
Se todos os elementos no modelo forem fixos, então o cálculo de estatística de F depende do que trata teste de hipótese, como se segue:
- F(Termo)
-

- F(teste de ajuste - Lack-of-fit)
-

Se houver fatores aleatórios no modelo, F é construído utilizando os dados de quadrado médio esperado para cada termo. Para obter mais informações, consulte Neter et al.1.
Notação
| Termo | Descrição |
|---|---|
| Termo de MS ajust | Uma medida da quantidade de variação que um termo explica após levar em conta os outros termos no modelo. |
| Erro de QM | Uma medida da variação de que o modelo não explica. |
| Falta de ajuste de QM | Uma medida da variação na resposta que poderia ser modelada adicionando-se mais termos ao modelo. |
| Erro puro de QM | Uma medida da variação em dados de resposta replicados. |
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Valor-p – Tabela Análise de Variância
O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:
- DF do numerador
- soma dos graus de liberdade para o termo ou os termos do teste
- DF do denominador
- graus de liberdade para erro
Fórmula
1 − P(F ≤ fj)
Notação
| Termo | Descrição |
|---|---|
| P(F ≤ f) | função de distribuição acumulada para a distribuição F |
| f | estatística F de teste |
