Neste tópico
S
S representa o desvio padrão da distância entre os valores dos dados e os valores ajustados. S é medida em unidades de resposta.
Interpretação
Use S para avaliar se o modelo descreve bem a resposta. S é medido nas unidades da variável de resposta e representa o quão longe os valores de dados caem dos valores ajustados. Quanto mais baixo for o valor de S, melhor o modelo descreve a resposta. No entanto, um valor de S baixo por si só não indica que o modelo satisfaz aos pressupostos do modelo. Você deve verificar os gráficos de resíduos para conferir os pressupostos.
Por exemplo, você trabalha para um fabricante de batatas fritas que examina os fatores que afetam a porcentagem de batatas quebradas por embalagem. Você reduz o modelo para os preditores significativos, e S é calculado como 1,79. Este resultado indica que o desvio padrão dos pontos de dados em torno dos valores ajustados é 1,79. Se você estiver comparando modelos, valores menores do que 1,79 indicam um ajuste melhor, e valores mais altos indicam um ajuste pior.
PRESS
A soma dos quadrados predita (PRESS) do erro é uma medida do desvio entre os valores ajustados e os valores observados. PRESS é semelhante à soma dos quadrados dos erros residuais (SSE), que é o somatório dos quadrados dos resíduos. No entanto, PRESS usa um cálculo diferente para os resíduos. A fórmula utilizada para calcular PRESS é equivalente a um processo para remover sistematicamente cada observação do conjunto de dados, estimando a equação de regressão, e determinando o quão bem o modelo prediz a observação removida.
Interpretação
Use PRESS para avaliar a capacidade de predição do modelo. Normalmente, quanto menor o valor PRESS, melhor a capacidade de predição do modelo. O Minitab usa o PRESS é usada para calcular o R2 predito, que é geralmente mais intuitivo para ser interpretado. Juntas, essas estatísticas podem evitar o excesso de ajuste do modelo. Um modelo com excesso de ajuste ocorre quando você adiciona termos a efeitos que não são importantes na população, embora eles possam parecer importantes nos dados da amostra. O modelo se adapta aos dados de amostra e, por conseguinte, pode não ser útil para fazer predições em relação à população.
R2
R2 representa a porcentagem de variação na resposta que é explicada pelo modelo. Ele é calculado como 1 menos a razão da soma dos quadrados dos erros (que é a variação que não é explicada pelo modelo) para a soma total dos quadrados (que é a variação total no modelo).
Interpretação
Use R2 para determinar se o modelo ajusta bem os dados. Quanto mais alto o valor de R2 melhor o modelo ajusta seus dados. O valor de R2 está sempre entre 0 e 100%.
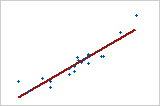
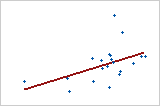
-
O R2 sempre aumenta quando você adiciona mais preditores a um modelo. Por exemplo, o melhor modelo de cinco preditores terá sempre um R2 que é pelo menos tão elevado quanto o melhor modelo de quatro preditores. Portanto, R2 é mais útil quando for comparado a modelos do mesmo tamanho.
-
Amostras pequenas não fornecem uma estimativa precisa da força da relação entre a resposta e os preditores. Por exemplo, se você precisar que R2 seja mais exato, deve usar uma amostra maior (geralmente, 40 ou mais).
-
A estatística de qualidade do ajuste é apenas uma medida do grau em que o modelo ajusta os dados (se ajusta bem ou mal). Mesmo quando um modelo tem um um valor desejável, você deve verificar os gráficos de resíduos para conferir se o modelo atende aos pressupostos do modelo.
R2 (pred)
O R2 predito é calculado com uma fórmula que é equivalente à remoção sistemática de cada observação do conjunto de dados, estimando a equação de regressão e determinando se o modelo faz (ou não) uma boa predição da observação removida. O valor do R2 predito varia entre 0% e 100%. (Enquanto os cálculos do R2 predito podem produzir valores negativos, o Minitab exibe zero para esses casos).
Interpretação
Use R2 predito para determinar o quão bem seu modelo prediz as respostas para novas observações. Modelos que têm valores de R2 predito mais elevado têm melhor capacidade preditiva.
Um R2 predito que é substancialmente menor que o R2 pode indicar que o modelo está com excesso de ajuste. Um modelo com excesso de ajuste ocorre quando você adiciona termos para efeitos que não são importantes na população. O modelo se adapta aos dados de amostra e, por conseguinte, pode não ser útil para fazer predições em relação à população.
O R2 previsto também pode ser mais útil do que o R2 ajustado para a comparação de modelos, porque ele é calculado com as observações que não estão incluídas no cálculo do modelo.
Por exemplo, um analista de uma empresa de consultoria financeira desenvolve um modelo para prever as condições futuras do mercado. O modelo parece promissor porque tem um R2 de 87%. No entanto, o R2 predito é apenas para 52%, o que indica que o modelo pode estar com excesso de ajuste.
R-sq (adj)
O R2 ajustado é a porcentagem de variação na resposta que é explicada pelo modelo, ajustada para o número de preditores do modelo em relação ao número de observações. O R2 ajustado é calculado como 1 menos a razão entre o quadrado médio do erro (QME) em relação ao quadrado médio total (QM total).
Interpretação
Use o R2 ajustado quando desejar comparar modelos que têm diferentes números de preditores. R2 sempre aumenta quando você adiciona um preditor ao modelo, mesmo quando não existe uma verdadeira melhoria ao modelo. O valor de R2 ajustado incorpora o número de preditores no modelo para ajudá-lo a escolher o modelo correto.
| Modelo | % Batata | Taxa de resfriamento | Temp de cozimento | R2 | R2 ajustado |
|---|---|---|---|---|---|
| 1 | X | 52% | 51% | ||
| 0 | X | X | 63% | 62% | |
| 3 | X | X | X | 65% | 62% |
O primeiro modelo produz um R2 de mais de 50%. O segundo modelo adiciona a taxa de resfriamento ao modelo. O R2 ajustado aumenta, o que indica que a taxa de resfriamento melhora o modelo. O terceiro modelo, o que aumenta a temperatura de cozimento, aumenta o R2, mas não o R2 ajustado. Esses resultados indicam que a temperatura de cozimento não aprimoram o modelo. Com base nesses resultados, você considera remover a temperatura de cozimento do modelo.
Cp de Mallows
A Cp de Mallows pode ajudar a escolher entre modelos de regressão múltipla concorrentes. A Cp de Mallows compara o modelo completo com os modelos com os subconjuntos de preditores. Ele ajuda a obter um equilíbrio importante com o número de preditores no modelo. Um modelo com preditores demais pode ser relativamente impreciso, enquanto um modelo com muito poucos preditores pode produzir estimativas viciadas. A utilização da Cp de Mallows para comparar modelos de regressão só é válida quando você começa com o mesmo conjunto completo de preditores.
Interpretação
Um valor de Cp de Mallows que está próximo do número de preditoras mais a constante indica que o modelo produz estimativas relativamente precisas e não-viciadas.
Um valor de Cp de Mallows que é maior que o número de preditores mais a constante indica que o modelo é viciado e não ajusta bem os dados.
