Neste tópico
Método
O Minitab usa dois métodos para analisar desvios-padrão da repetição ou medições da replicação: mínimos quadrados e máxima verossimilhança. Ambos os métodos baseiam-se em um modelo linear com uma função de ligação de log: ln (σ) = Aγ, em que A é a matriz do experimento e γ é um vetor de parâmetros a ser estimado. Uma vantagem de usar a função de ligação de log é que os valores ajustados são sempre positivos.
Os dois métodos produzem resultados equivalentes no modelo saturado quando o número de parâmetros é igual ao número de pontos de dados.
Para a estimativa de mínimos quadrados, o Minitab usa regressão de mínimos quadrados ponderados. Se o número de repetições ou replicações for o mesmo, os pesos são iguais.
Para MLE, o Minitab assume que os dados originais são provenientes de uma distribuição normal. A distribuição da variância da amostra está relacionada com a distribuição χ2.
Matriz de experimento
Minitab usa a mesma abordagem para a matriz de experimento que é usada no modelo linear generalizado (GLM), que usa a regressão para ajustar o modelo especificado. Primeiro, o Minitab cria uma matriz de experimento a partir dos fatores e do modelo que você especificar. As colunas desta matriz, chamada X, representam os termos no modelo.
A matriz do experimento tem n linhas, onde n = número de observações e vários blocos de colunas, o que corresponde aos termos do modelo. O primeiro bloco é para a constante e contém apenas uma coluna, uma coluna para todos eles. O bloco para um fator de contínuo também contém apenas uma coluna. O bloco de colunas para um fator categórico contém r colunas, onde r = graus de liberdade para o fator.
Por exemplo, um experimento fatorial fracionado possui três fatores com 2 níveis cada. O modelo inclui 3 efeitos principais. Cada linha é codificada como uma das opções a seguir:
| Blocos | Fator 1 | Fator 2 | Fator 3 |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 1 | 1 | −1 | −1 |
| 1 | −1 | 1 | −1 |
| 1 | 1 | 1 | −1 |
| 1 | −1 | −1 | 1 |
| 1 | 1 | −1 | 1 |
| 1 | −1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Efeitos
Os efeitos estimados para cada fator. Os efeitos só são calculados para modelos em dois níveis e não são calculados para modelos fatoriais gerais. A fórmula para o efeito de um fator é:
Efeito = Coeficiente * 2
Coeficientes (Coef)
As estimativas dos coeficientes de regressão populacional em uma equação de regressão. Para cada um dos fatores, o Minitab calcula k - 1 coeficientes, onde k é o número de níveis no fator. Para um modelo fatorial com 2 fatores, 2 níveis e completo, as fórmulas para os coeficientes para os fatores e interações são:


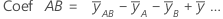
O erro padrão do coeficiente para este modelo fatorial com 2 fatores, 2 níveis e completo é:

Para obter mais informações sobre os modelos com mais de dois fatores ou fatores com mais de dois níveis, consulte Montgomery1.
Notação
| Termo | Descrição |
|---|---|
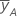 | média de y com alto nível de fator A |
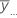 | média global de todas as observações |
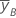 | média de y com alto nível de fator B |
 | média de y com altos níveis de A e B |
| MSE | quadrado médio do erro |
| n | número de - 1 e 1 (na matriz de covariância) para o termo estimado |
Regressão ponderada
A regressão de mínimos quadrados ponderada é um método para lidar com as observações que têm variâncias não constantes. Se as variâncias são não constantes, observações com:
- grandes variâncias devem ser dadas em relação a pesos pequenos
- pequenas variâncias devem ser dadas em relação a pesos grandes
Os pesos refletem o número de repetições ou replicações utilizadas para calcular cada desvio padrão. Os desvios padrão com base em dados mais recebem pesos maiores.
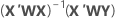
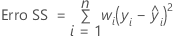
Notação
| Termo | Descrição |
|---|---|
| X | matriz de planejamento |
| X' | transposição da matriz do experimento |
| W | uma matriz n x n com os pesos na diagonal |
| Y | vetor de valores de desvio padrão do log |
| n | número de observações |
| wi | peso para a ia observação |
| yi | valor de desvio padrão do log para a ia observação |
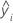 | valor ajustado para o desvio padrão do log para a ia observação |
Cálculo de pesos
É possível calcular e armazenar pesos usando variâncias adaptadas ou ajustadas com base no modelo de dispersão para ser utilizado ao analisar o modelo de localização.
- 1 / variância ajustada
- σ2(entre) + σ2 (dentro) / número de repetições
"Entre" e "dentro" referem-se a um ensaio do experimento. A variação dentro de um ensaio é o que você medir com o desvio padrão para observações repetidas. A variação entre ensaios refere-se as fontes de variação adicionais para novos ensaios.
Quando você analisa o desvio padrão em todas as repetições, está ajustando um modelo para s (dentro). Se você tiver replicações, o Minitab combina o modelo de σ2 (dentro) e a variância de médias nas replicações para obter uma estimativa de σ2 (entre). Então, a estimativa de σ2 (entre) é recombinada com σ2 (dentro) / número de repetições para obter as estimativas de variância para as médias que são consistentes com seu modelo de dispersão.
Esta abordagem assume que σ2(entre) é constante e não depende dos níveis de fator. Se essa suposição for incorreta, você pode querer ajustar um modelo para a variância de x usando as respostas de pré-processamento com  para obter σ2 entre as replicações.
para obter σ2 entre as replicações.
Se você tiver covariáveis no modelo, deve explicá-las na variância para repetições. Você não pode ser responsável por covariáveis na variância ajustada.
