Neste tópico
Soma de quadrados (SS)
A soma das distâncias ao quadrado. As fórmulas apresentados são para um modelo fatorial completo, de dois fatores com os fatores A e B. Estas fórmulas podem ser estendidas para modelos com mais de dois fatores. Para obter informações, consulte Montgomery1.
O SS Total é a variação total no modelo. SS (A) e SS (B) são a soma dos desvios quadrados das médias de nível de fator estimado em torno da média global. SS Erro é a soma dos quadrados dos resíduos. Também é conhecido como erro dentro de tratamentos. Os cálculos são:



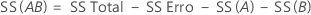


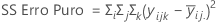

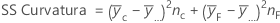


- D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition, John Wiley & Sons.
Notação
| Termo | Descrição |
|---|---|
| a | número de níveis no fator A |
| b | número de níveis no fator B |
| n | número total de replicações |
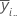 | média do io nível de fator A |
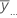 | média global de todas as observações |
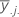 | média do jo nível de fator B |
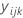 | observação do io nível de fator A, jo nível de fator B e a ka replicação |
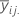 | média do io nível do fator A e jo nível do fator B |
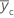 | resposta média para os pontos centrais |
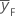 | resposta média para os pontos fatoriais |
| nF | número de pontos fatoriais |
Soma dos quadrados sequencial
O Minitab decompõe a o componente de Regressão SS ou Tratamentos da variância em somas dos quadrados sequenciais para cada fator. As somas dos quadrados sequenciais dependem da ordem dos fatores preditores e são inseridas no modelo. A soma dos quadrados sequencial é a parte única da Regressão SS explicada por um fator, considerando-se todos os fatores inseridos anteriormente.
Por exemplo, se você tem um modelo com três fatores ou preditores, X1, X2 e X3, a soma dos quadrados sequencial para X2 mostra quanto da variação restante é explicada por X2, considerando-se que X1 já está no modelo. Para obter uma sequência de fatores diferente, repita a análise e insira os elementos em uma ordem diferente.
Soma dos quadrados ajustada
A soma dos quadrados ajustada não depende da ordem em que os termos são inseridos no modelo. A soma dos quadrados ajustada é a quantidade de variação explicada por um termo, tendo em conta todos os outros termos no modelo, independentemente da ordem em que os termos entram no modelo.
Por exemplo, se você tem um modelo com três fatores, X1, X2 e X3, a soma ajustada dos quadrados para X2 mostra quanto da variação restante do termo para X2 é explicada, considerando-se que os termos para X1 e X3 já estão no modelo.
Os cálculos para as somas dos quadrados ajustado para três fatores são:
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) ou
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
em que SSR(X3 | X1, X2) é a soma dos quadrados ajustada para X3, dado que X1 e X2 estão no modelo.
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) ou
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
em que SSR(X2, X3 | X1) é a soma dos quadrados ajustados para X2 e X3, dado que X1 está no modelo.
Você pode estender estas fórmulas se tiver mais de 3 fatores em seu modelo1.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Graus de liberdade (DF)
Para um experimento fatorial completo com fatores A e B, e uma variável de bloqueio, o número de graus de liberdade associados com cada soma dos quadrados é:





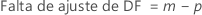

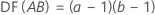
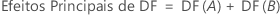
Para experimentos de dois níveis com pontos centrais, os graus de liberdade para a curvatura têm valor 1.
Notação
| Termo | Descrição |
|---|---|
| a | número de níveis no fator A |
| b | número de níveis no fator B |
| c | número de blocos |
| n | número total de observações |
| ni | número de observações para a io combinação de níveis de fatores |
| m | número de combinações de nível de fator |
| p | número de coeficientes |
MS Aj – Termo

F
Um teste para determinar se a interação e os efeitos principais são significativos. A fórmula para os termos do modelo é:

Os graus de liberdade do teste são:
- Numerador = graus de liberdade do termo
- Denominador = graus de liberdade do erro
Valores maiores de suporte de F rejeitam a hipótese nula de que não existe um efeito significativo.
Para experimentos subdivididos balanceados, a estatística F para os fatores de difícil alteração usa o MS para erro da parcela integral no denominador. Para outros experimentos subdivididos, o Minitab usa uma combinação linear do erro de parcelas integrais e do erro de parcelas subdivididas para criar um denominador baseado nas expectativas dos quadrados médios.
Valor-p – Tabela Análise de Variância
O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:
- DF do numerador
- soma dos graus de liberdade para o termo ou os termos do teste
- DF do denominador
- graus de liberdade para erro
Fórmula
1 − P(F ≤ fj)
Notação
| Termo | Descrição |
|---|---|
| P(F ≤ f) | função de distribuição acumulada para a distribuição F |
| f | estatística F de teste |
Teste de ajuste (lack-of-fit) de erro puro
- A soma dos desvios quadrados da resposta da média dentro de cada conjunto de replicações adiciona-os juntos para criar a soma dos quadrados do erro puro (SS PE).
- O quadrado médio do erro puro
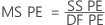

onde n = número de observações e m = número de combinações de nível x distintas
- A soma dos quadrados do teste de ajuste (lack-of-fit)
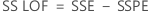
- O quadrado médio do teste de ajuste (lack-of-fit)

- A estatística de teste

Valores de F altos e valores de p baixos sugerem que o modelo é inadequado.
Valor-p – teste de ajuste (lack-of-fit)
- DF do numerador
- graus de liberdade do teste de ajuste (lack-of-fit)
- DF do denominador
- graus de liberdade para erro puro
Fórmula
1 − P(F ≤ fj)
Notação
| Termo | Descrição |
|---|---|
| P(F ≤ fj) | função de distribuição acumulada para a distribuição F |
| fj | estatística F de teste |
