Um engenheiro de qualidade de um fabricante de produtos de construção está desenvolvendo um novo produto de isolamento. O engenheiro cria um experimento fatorial completo em 2 níveis para estudar os efeitos de vários fatores na variação da resistência do isolamento. Ao realizar o experimento de resistência, o engenheiro decide coletar amostras extras para examinar os efeitos dos fatores na variabilidade na resistência do isolamento. O engenheiro coleta seis medições repetidas de resistência em cada combinação de configurações de fator e calcula o desvio padrão das repetições.
O engenheiro analisa a variabilidade um experimento fatorial para determinar como o tipo de material, a pressão de injeção, a temperatura de injeção e a temperatura de arrefecimento afetam a variabilidade na resistência do isolamento.
- Abra os dados amostrais, ResistênciaDoIsolamento.MWX.
- Conclua Exemplo de Respostas do pré-processo para análise de variabilidade.
- Selecione .
- Em Resposta (desvios padrão):, insira Pad.
- Clique em Termos.
- Em Incluir termos no modelo por toda a ordem, Escolha 2 na lista suspensa. Clique em OK.
- Clique em Gráficos.
- Em Gráficos de Efeitos, selecione Pareto.
- Em Gráficos de Resíduos, selecione Três em um.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
Na análise da Tabela de Variância, o valor-p para o efeito principal do Material e a interação Material*InjPress são significativos no nível α de 0,05. O engenheiro pode considerar a redução do modelo.
O valor de R2 mostra que o modelo explica 97,75% da variância em resistência, o que indica que o modelo ajusta os dados extremamente bem.
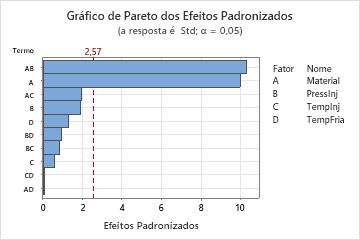
O gráfico de Pareto dos efeitos possibilita a identificação visual dos efeitos importantes e compara a magnitude relativa dos vários efeitos. Além disso, é possível ver que o maior efeito é Material*InjPress (AB) porque se estende para mais distante. Material*CoolTemp (AD) é o menor porque se estende menos.
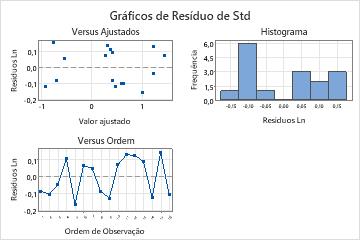
Os gráficos de resíduos não indicam nenhum problema com o modelo.
Método
| Estimação | Mínimos quadrados |
|---|
Coeficientes Codificados para Ln(Std)
| Termo | Efeito | Razão de Efeitos | Coef | EP de Coef | Valor-T | Valor-P | VIF |
|---|---|---|---|---|---|---|---|
| Constante | 0,3424 | 0,0481 | 7,12 | 0,001 | |||
| Material | -0,9598 | 0,3830 | -0,4799 | 0,0481 | -9,99 | 0,000 | 1,00 |
| PressInj | -0,1845 | 0,8315 | -0,0922 | 0,0481 | -1,92 | 0,113 | 1,00 |
| TempInj | 0,0555 | 1,0571 | 0,0278 | 0,0481 | 0,58 | 0,589 | 1,00 |
| TempFria | -0,1259 | 0,8817 | -0,0629 | 0,0481 | -1,31 | 0,247 | 1,00 |
| Material*PressInj | -0,9918 | 0,3709 | -0,4959 | 0,0481 | -10,32 | 0,000 | 1,00 |
| Material*TempInj | 0,1875 | 1,2062 | 0,0937 | 0,0481 | 1,95 | 0,109 | 1,00 |
| Material*TempFria | 0,0056 | 1,0056 | 0,0028 | 0,0481 | 0,06 | 0,956 | 1,00 |
| PressInj*TempInj | -0,0792 | 0,9239 | -0,0396 | 0,0481 | -0,82 | 0,448 | 1,00 |
| PressInj*TempFria | -0,0900 | 0,9139 | -0,0450 | 0,0481 | -0,94 | 0,392 | 1,00 |
| TempInj*TempFria | 0,0066 | 1,0066 | 0,0033 | 0,0481 | 0,07 | 0,948 | 1,00 |
Sumário do Modelo para Ln(Std)
| S | R2 | R2(aj) | R2(pred) |
|---|---|---|---|
| 0,549040 | 97,75% | 93,25% | 76,97% |
Análise de Variância para Ln(Std)
| Fonte | GL | SQ (Aj.) | QM (Aj.) | Valor F | Valor-P |
|---|---|---|---|---|---|
| Modelo | 10 | 65,4970 | 6,5497 | 21,73 | 0,002 |
| Linear | 4 | 31,7838 | 7,9459 | 26,36 | 0,001 |
| Material | 1 | 30,0559 | 30,0559 | 99,71 | 0,000 |
| PressInj | 1 | 1,1104 | 1,1104 | 3,68 | 0,113 |
| TempInj | 1 | 0,1005 | 0,1005 | 0,33 | 0,589 |
| TempFria | 1 | 0,5170 | 0,5170 | 1,71 | 0,247 |
| Interações de 2 fatores | 6 | 33,7132 | 5,6189 | 18,64 | 0,003 |
| Material*PressInj | 1 | 32,0953 | 32,0953 | 106,47 | 0,000 |
| Material*TempInj | 1 | 1,1466 | 1,1466 | 3,80 | 0,109 |
| Material*TempFria | 1 | 0,0010 | 0,0010 | 0,00 | 0,956 |
| PressInj*TempInj | 1 | 0,2046 | 0,2046 | 0,68 | 0,448 |
| PressInj*TempFria | 1 | 0,2642 | 0,2642 | 0,88 | 0,392 |
| TempInj*TempFria | 1 | 0,0014 | 0,0014 | 0,00 | 0,948 |
| Erro | 5 | 1,5072 | 0,3014 | ||
| Total | 15 | 67,0043 |
Equação de Regressão em Unidades Não codificadas
| Ln(Std) | = | -1,30 - 0,158 Material + 0,0148 PressInj + 0,0180 TempInj + 0,0031 TempFria - 0,01322 Material*PressInj + 0,01250 Material*TempInj + 0,00028 Material*TempFria - 0,000141 PressInj*TempInj - 0,000120 PressInj*TempFria + 0,000044 TempInj*TempFria |
|---|
Estrutura de Aliases
| Fator | Nome |
|---|---|
| A | Material |
| B | PressInj |
| C | TempInj |
| D | TempFria |
| Aliases |
|---|
| I |
| A |
| B |
| C |
| D |
| AB |
| AC |
| AD |
| BC |
| BD |
| CD |