Métodos e fórmulas para método de análise de variância em Análise da resposta binária para experimentos fatoriais

A desviância mede a discrepância entre o modelo atual e o modelo completo. O modelo completo é o modelo que tem n parâmetros, um parâmetro por observação. O modelo completo maximiza a função log-verossimilhança. O modelo completo fornece um ponto de comparação para modelos com menos de n parâmetros. As comparações ao modelo completo usam desviância escalada.

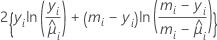
A tabela de desviância é construída com base no seguinte resultado geral que supõe que ϕ é conhecido. Se D_I for a desviância associada a um modelo inicial e D_S for a desviância associada a um subconjunto de termos no modelo inicial, sob algumas condições de regularidade, a seguinte relação existe:

A diferença entre as desviâncias é assintoticamente distribuída como uma distribuição qui-quadrado com d graus de liberdade. Essas estatísticas são calculadas para análise ajustada (tipo III) e análise sequencial (tipo I). A desviância ajustada e a estatística qui-quadrado na tabela de desviâncias são iguais. A desviância média ajustada é a desviância ajustada dividida pelos graus de liberdade.

Para a análise sequencial, a saída depende da ordem em que as preditoras entram no modelo. A desviância sequencial é a parte exclusiva da desviância que uma preditora explica, dadas quaisquer preditoras já no modelo. Se você tiver um modelo com três preditoras, X1, X2 e X3, a desviância sequencial para X3 mostra quanto da desviância restante que X3 explica, dado que X1 e X2 já estejam no modelo. Para obter uma desviância sequencial diferente, repita o procedimento de regressão inserindo as preditoras em uma ordem diferente.

Se ϕ for desconhecido, quanto às respostas que seguem uma distribuição normal, sob algumas condições de regularidade, a relação muda para o seguinte:

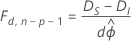
Aqui, a diferença entre as desviâncias é assintoticamente distribuída como uma distribuição F com d graus de liberdade para o numerador e n − p graus de liberdade para o denominador. Para estimar o parâmetro de dispersão, use o modelo inicial.

Notação

Termo	Descrição
yi	o número de eventos da iésima linha
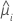	a resposta média estimada da iésima linha
mi	o número de ensaios da iésima linha
Lf	a log-verossimilhança do modelo completo
Lc	a log-verossimilhança do modelo com um subconjunto de termos do modelo completo
d	os graus de liberdade são a diferença entre os números de parâmetros nos modelos a comparar
ϕ	o parâmetro de dispersão, conhecido por ser 1 para o modelo binomial
n	o número de linhas nos dados
p	os graus de liberdade da regressão do modelo inicial

Indica o número de informações independentes que envolvem os dados de resposta necessários para calcular as desviâncias médias ajustados. Os graus de liberdade para cada componente do modelo são:

Notação

Termo	Descrição
p	A soma dos graus de liberdade das preditoras. As preditoras não incluem a constante.
n	O número de linhas no experimento
q	O número de níveis da preditora categórica
b	O número de blocos
a	O número de níveis no fator A
b	O número de níveis no fator B

As funções de log-verossimilhança são parametrizadas nos termos das médias. A forma geral das funções são as seguintes:

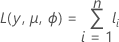
A forma geral das contribuições individuais são as seguintes:

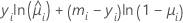
Notação

Termo	Descrição
yi	o número de eventos da iésima linha
mi	o número de ensaios da iésima linha
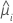	a resposta média estimada da iésima linha

Usado nos testes de hipóteses para ajudá-lo a decidir se deve rejeitar ou não rejeitar uma hipótese nula. O valor-p é a probabilidade de se obter uma estatística de teste que seja pelo menos tão extrema quanto o valor calculado real, se a hipótese nula for verdadeira. Um valor cortado comumente usado para o valor-p é 0,05. Por exemplo, se o valor-p calculado de uma estatística de teste for menor do que 0,05, você rejeita a hipótese nula.