R2 da desviância
O R2 da desviância geralmente é considerado a proporção total da desviância na variável resposta que explica o modelo.
Interpretação
Normalmente, quanto maior o R2 de deviance, melhor o modelo ajusta os dados. O R2 de deviance está sempre entre 0 e 100%.
O R2 da desviância sempre aumenta quando são adicionados termos a um modelo. Por exemplo, o melhor modelo com 5 termos sempre terá um R2 que pelo menos tão alto quanto o melhor modelo com 4 termos. Portanto, R2 da desviância é mais útil quando for comparado a modelos do mesmo tamanho.
A estatística de qualidade do ajuste é apenas uma medida do grau em que o modelo ajusta os dados (se ajusta bem ou mal). Mesmo quando um modelo tem um valor desejável, você deve verificar os gráficos de resíduos e testes de qualidade do ajuste para avaliar se um modelo ajusta bem os dados.
Você pode usar um gráfico de linhas ajustado para ilustrar graficamente valores de R2 da desviância. O primeiro gráfico ilustra um modelo que explica aproximadamente 96% da desviância na resposta. O segundo gráfico ilustra um modelo que explica cerca de 60% da desviância na resposta. Quanto mais desviância um modelo explica, mais próximos os pontos de dados caem na curva. Teoricamente, se um modelo pudesse explicar 100% da desviância, os valores ajustados seriam sempre iguais aos valores observados e todos os pontos de dados cairiam na curva.
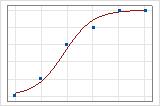
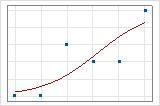
O arranjo dos dados afeta o valor de R2 da desviância. O R2 da desviância normalmente é mais alto para dados com múltiplos ensaios por linha que para dados com um único ensaio por linha. Os valores de R2 da desviância só são comparáveis entre os modelos que usam o mesmo formato de dados. Para obter mais informações, acesse Como os formatos de dados afetam a qualidade de ajuste na regressão logística binária.
R2 (aj) da desviância
O R2 de deviance ajustado representa a porcentagem de desvio na resposta que é explicada pelo modelo, ajustada para o número de preditores do modelo em relação ao número de observações.
Interpretação
Use o R2 do deviance ajustado para comparar modelos que têm número de termos diferentes. O R2 de deviance sempre aumenta quando você adiciona um termo ao modelo. O valor de R2 da desviância ajustado incorpora o número de termos no modelo para ajudá-lo a escolher o modelo correto.
| Passo | % Batata | Taxa de resfriamento | Temp de cozimento | desviância R2 | desviância ajustada R2 | Valor-p |
|---|---|---|---|---|---|---|
| 1 | X | 52% | 51% | 0,000 | ||
| 0 | X | X | 63% | 62% | 0,000 | |
| 3 | X | X | X | 65% | 62% | 0,000 |
A primeira etapa produz um modelo de regressão estatisticamente significativo. A segunda etapa, que adiciona uma taxa de resfriamento ao modelo, aumenta o R2 da desviância ajustado, que indica que a taxa de resfriamento aprimora o modelo. A terceira etapa, que adiciona temperatura de cozimento ao modelo, aumenta o R2 da desviância, mas não o R2 da desviância ajustado. Esses resultados indicam que a temperatura de cozimento não aprimoram o modelo. Com base nesses resultados, você considera remover a temperatura de cozimento do modelo.
O arranjo dos dados afeta o valor de R2 da desviância ajustado. Para os mesmos dados, o R2 da desviância ajustado normalmente é mais alto para dados com múltiplos ensaios por linha que para dados com um único ensaio por linha. Use o R2 da desviância ajustado somente para comparar o ajuste dos modelos que têm o mesmo formato de dados. Para obter mais informações, acesse Como os formatos de dados afetam a qualidade de ajuste na regressão logística binária.
AIC, AICc e BIC
O Critério de Informação de Akaike (AIC), o Critério de Informação de Akaike Corrigido (AICc) e o Critério de Informação Bayesiano (BIC) são medidas da qualidade relativa de um modelo que consideram o ajuste e a quantidade de termos no modelo.
Interpretação
- AICc e BIC
- Quando o tamanho da amostra é pequeno em relação aos parâmetros do modelo, o AICc funciona melhor do que o AIC. AICc funciona melhor porque, com tamanhos de amostra relativamente pequenos, o AIC tende a ser pequeno para modelos com muitos parâmetros. Em geral, as duas estatísticas dão resultados semelhantes quando o tamanho da amostra é grande o bastante em relação aos parâmetros no modelo.
- AICc e BIC
- Tanto AICc como BIC avaliam a verossimilhança do modelo e aplicam uma penalidade para adicionar termos ao modelo. Tal penalidade reduz a tendência de sobreajuste do modelo aos dados amostrais. Essa redução pode produzir um modelo com melhor desempenho geral.
