Neste tópico
Efeito
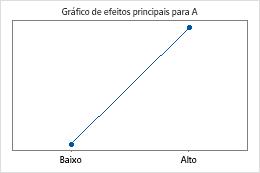
Um efeito descreve o tamanho e a direção da relação entre um termo e a variável de resposta. O Minitab calcula os efeitos de fatores e as interações entre fatores.
Interpretação
O tamanho do efeito corresponde a uma alteração na função de ligação. Ao usar a função de ligação logit, o tamanho do efeito é o log de razão de chances para a mudança de baixo para alto nível do fator. O sinal do efeito indica a direção da relação entre o termo e a resposta.
Com mais fatores em uma interação, há mais dificuldade em interpretar o efeito. Para os fatores e as interações entre fatores, o tamanho do efeito é, em geral, uma boa maneira de avaliar o a significância prática do efeito que um termo exerce sobre variável de resposta.
O tamanho do efeito não indica se um termo é estatisticamente significativo porque os cálculos para significância também consideram a variação nos dados de resposta. Para determinar a significância estatística, examine o valor-p para o termo.
Coef
Um coeficiente de regressão descreve o tamanho e a direção da relação entre um preditor e variável de resposta. Os coeficientes são os números pelos quais os valores do termo são multiplicados em uma equação de regressão.
Interpretação
Use o coeficiente para determinar se uma mudança na variável preditora pode tornar o evento mais ou menos provável. O coeficiente de um termo representa a alteração na função de ligação associada com um aumento de uma unidade codificada naquele termo, enquanto os outros termos no modelo são mantidos constantes.
O tamanho do efeito é, em geral, uma boa maneira de avaliar a significância prática do efeito que um termo exerce sobre a variável de resposta. O tamanho do efeito não indica se um termo é estatisticamente significativo porque os cálculos para significância também consideram a variação nos dados de resposta. Para determinar a significância estatística, examine o valor-p para o termo.
A relação entre o coeficiente e a probabilidade depende de diversos aspectos da análise, incluindo a função de ligação, o evento de referência da resposta e os níveis de referência das preditoras categóricas que estão no modelo. Geralmente, os coeficientes positivos tornam o evento mais provável e os coeficientes negativos tornam o evento menos provável. Um coeficiente estimado próximo de 0 sugere que o efeito do preditor é pequeno.
- Covariáveis
- O coeficiente para uma covariável está nas mesmas unidades que a covariável. O coeficiente representa a alteração na função de ligação para o aumento de uma unidade na covariável. Se o coeficiente for negativo, conforme a covariável aumenta, a probabilidade diminui. Se o coeficiente for positivo, conforme aumenta a covariável, a probabilidade aumenta. Como as covariáveis não são codificadas e normalmente não são ortogonais em relação aos fatores, a presença de covariáveis, em geral, aumenta os valores do VIF. Para obter mais informações, acesse a seção sobre VIF.
- Blocos
- Os blocos são variáveis categóricas com um esquema de codificação (-1, 0, +1). Cada coeficiente representa a diferença entre a função de ligação para o bloco e o valor médio.
- PtCentral
- O termo do ponto central é codificado como 1 para um ponto central e como 0 para outros pontos. Em geral, o coeficiente do termo CenterPt não é interpretado porque o termo representa tantos efeitos quadrático confundidos quantos fatores houver no experimento. Normalmente, você usa o valor-p para determinar o valor de uma maior coleta de dados para estimar os efeitos quadráticos dos fatores.
Interpretação da função de ligação logit
A função de ligação logit fornece a interpretação mais natural dos coeficientes estimados e é, portanto, a ligação padrão no Minitab. A interpretação usa o fato que a chance de um evento de referência ser P(evento)/P(não-evento) e assume que os outros preditores permanecem constantes. Quanto maior for a chance do log, mais provável o evento de referência será. Portanto, coeficientes positivos indicam que o evento se torna mais provável e coeficientes negativos indicam que o evento se torna menos provável. Um resumo das interpretações para diferentes tipos de fatores está a seguir.
- Fatores contínuos
- O coeficiente de um fator contínuo é a mudança estimada no log natural da chance para o evento de referência do aumento de uma unidade codificada no fator. Por exemplo, se cada unidade codificada de um fator de tempo representa uma alteração de 30 segundos e o coeficiente para o tempo é 1,4, então o log natural da chance aumenta 1,4 se o tempo for aumentado em 30 segundos.
- Fatores categóricos
- Para um fator de 2 níveis, a interpretação do coeficiente de um fator categórico pode estar entre os dois níveis. O coeficiente de um fator categórico é a mudança estimada no registro natural das chances do evento para uma mudança de uma unidade codificada. A diferença entre os níveis baixo e alto de um fator categórico é de 2 unidades codificadas. Por exemplo, uma variável categórica possui os níveis Rápido e Lento. Lento é o nível baixo, codificado como -1. Rápido é o nível alto, codificado como +1. Se o coeficiente da variável for 1,3, a mudança de Lento para Rápido aumenta o log natural das probabilidades do evento em 2,6.
Coeficiente de SE
O erro padrão do coeficiente estima a variabilidade entre a estimativa do coeficiente que seria obtida caso fossem extraídas amostras da mesma população por vezes seguidas. O cálculo pressupõe que o tamanho da amostra e os coeficientes para estimativa permaneceriam os mesmos caso fossem extraídas repetidas amostras.
Interpretação
Use o erro padrão do coeficiente para medir a precisão da estimativa do coeficiente. Quanto menor o erro padrão, mais precisa é a estimativa.
Intervalo de confiança para coeficiente (IC de 95%)
Estes intervalos de confiança (IC) são amplitudes de valores que apresentam a probabilidade de conter o verdadeiro valor de cada termo no modelo.
Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. No entanto, se você extrair muitas amostras aleatórias, uma determinada porcentagem dos intervalos de confiança resultantes conterá o parâmetro populacional desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
- Estimativa de ponto
- Este valor único estima um parâmetro populacional usando os seus dados amostrais.
- Margem de erro
- A margem de erro define a largura do intervalo de confiança e é afetada pela amplitude das probabilidades do evento, o tamanho amostral e o nível de confiança.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do coeficiente de população para cada termo no modelo.
Por exemplo, com um nível de confiança de 95%, é possível ter 95% de certeza de que o intervalo de confiança contém o valor da razão de chances para a população. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
Valor Z
O valor Z é uma estatística de teste para testes de Wald que mede a razão entre o coeficiente e seu erro padrão.
Interpretação
O Minitab usa o valor Z para calcular o valor-p, que pode ser usado para a tomada de uma decisão sobre a significância estatística dos termos e do modelo. O teste de Wald é exato quando o tamanho da amostra é grande o bastante de forma que a distribuição dos coeficientes da amostra segue uma distribuição normal.
Um valor-z que está suficientemente longe de 0 indica que a estimativa do coeficiente é amplo e preciso o bastante para ser estatisticamente diferente de 0. Inversamente, um valor-z que está perto de 0 indica que a estimativa do coeficiente é muito pequena ou muito imprecisa para estar certa de que o termo tem um efeito na resposta.
Os testes na tabela Deviance são testes da razão de verossimilhança. O teste na exibição expandida da tabela Coeficientes são os testes de aproximação Wald. Os testes da razão de verossimilhança são mais precisos para amostras pequenas do que os testes de aproximação Wald.
Valor-p
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Os testes na tabela Deviance são testes da razão de verossimilhança. O teste na exibição expandida da tabela Coeficientes são os testes de aproximação Wald. Os testes da razão de verossimilhança são mais precisos para amostras pequenas do que os testes de aproximação Wald.
Interpretação
Para determinar se um coeficiente é estatisticamente diferente de 0, compare o valor-p do prazo com seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula é que o coeficiente é igual a zero, o que implica a não existência de uma associação entre o termo e a resposta.
Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de se concluir que o coeficiente não é 0 quando, na verdade, ele é.
- Valor-p ≤ α: a associação é estatisticamente significativa
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo.
- Valor-p > α: a associação não é estatisticamente significativa
- Se o valor-p for maior ou igual ao nível de significância, não é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo. Talvez seja necessário reajustar o modelo sem o termo.
- Fatores
- Se o coeficiente de um fator for significativo, é possível concluir que a probabilidade do evento não é a mesma para todos os níveis do fator.
- Interações entre fatores
- Se o coeficiente para uma interação for estatisticamente significativo, é possível concluir que a relação entre um fator e a resposta depende dos outros fatores no termo.
- Covariáveis
- Se o coeficiente de uma covariável for estatisticamente significativo, é possível concluir que a associação entre a resposta e a covariável é estatisticamente significativa.
- Blocos
- Se o coeficiente de um bloco for estatisticamente significativo, é possível concluir que a função de ligação do bloco é diferente do valor médio.
- PtCentral
- Se o coeficiente para um ponto central for estatisticamente significativo, é possível concluir que pelo menos um dos fatores tem uma relação curva com a resposta. Talvez você queira adicionar pontos axiais ao experimento para poder modelar a curvatura.
Interpretação da função de ligação logit
A função de ligação logit fornece a interpretação mais natural dos coeficientes estimados e é, portanto, a ligação padrão no Minitab. A interpretação usa o fato que a chance de um evento de referência ser P(evento)/P(não-evento) e assume que os outros preditores permanecem constantes. Quanto maior for a chance do log, mais provável o evento de referência será. Portanto, coeficientes positivos indicam que o evento se torna mais provável e coeficientes negativos indicam que o evento se torna menos provável. Um resumo das interpretações para diferentes tipos de fatores está a seguir.
- Fatores contínuos
- O coeficiente de um fator contínuo é a mudança estimada no log natural da chance para o evento de referência do aumento de uma unidade codificada no fator. Por exemplo, se cada unidade codificada de um fator de tempo representa uma alteração de 30 segundos e o coeficiente para o tempo é 1,4, então o log natural da chance aumenta 1,4 se o tempo for aumentado em 30 segundos.
- Fatores categóricos
- Para um fator com 2 níveis, a interpretação do coeficiente de um fator categórico pode estar entre os dois níveis. O coeficiente de um fator categórico é a mudança estimada entre o log natural da chance para o evento para uma mudança de uma unidade codificada. A diferença entre os níveis alto e baixo de um fator categórico é de 2 unidades codificadas. Por exemplo, uma variável categórica tem os níveis Rápido e Lento. Lento é o nível baixo, codificado como -1. Rápido é o nível alto, codificado como +1. Se o coeficiente para a variável for 1,3 então a mudança de Lento para Rápido aumenta o log natural da chance do evento em 2,6.
VIF
O fator de inflação da variância (VIF) indica o quanto a variação de um coeficiente é inflado devido a correlações entre os preditores no modelo.
Interpretação
Use o VIF para descrever quanta multicolinearidade (que é correlação entre preditores) existe em um modelo. Todos os valores de VIF são 1 na maioria dos experimentos fatoriais, indicando que os preditores não têm nenhuma multicolinearidade. A ausência de multicolinearidade simplifica a determinação de significância estatística. A inclusão de covariáveis no modelo e a ocorrência de ensaios danificados durante a coleta de dados são duas maneiras comuns pelas quais os valores de VIF aumentam, o que complica a interpretação de significância estatística.
| VIF | Status do preditor |
|---|---|
| VIF = 1 | Não correlacionados |
| 1 < VIF < 5 | Moderadamente correlacionados |
| VIF > 5 | Altamente correlacionados |
- Pode parecer que os coeficientes não são eventos estatisticamente significativos quando existe uma relação importante entre o preditor e da resposta.
- Coeficientes para preditores altamente correlacionados variam fortemente de amostra para amostra.
- A remoção de quaisquer termos altamente correlacionadas do modelo afetará significativamente os coeficientes estimados dos outros termos altamente correlacionados. Os coeficientes dos termos altamente correlacionadas podem até mudar a direção do efeito.
Seja cauteloso ao usar significância estatística para escolher os termos a serem removidos de um modelo quando houver multicolinearidade. Adicione e remova apenas um termo de cada vez do modelo. Monitore as mudanças nas estatísticas de resumo do modelo, bem como os testes de significância estatística, conforme você muda o modelo.
