Tabela Análise de Variância para Análise da resposta binária para experimentos fatoriais

Encontre definições e orientações de interpretação para cada estatística na tabela Análise de Variância.

Neste tópico

DF
Dev. seq.
Contribuição
Dev. aj.
Média aj.

Qui-quadrado
Valor-p – Modelo
Valor-p – termo
Valor-p – Curvatura

DF

O total de graus de liberdade (DF) corresponde a quantidade de informações em seus dados. A análise usa essa informação para estimar os valores dos coeficientes. O total de DF é 1 a menos que o número de linhas nos dados. O DF de um termo mostra quantos coeficientes esse termo usa. Aumentar o número de termos em seu modelo adiciona mais coeficientes ao modelo, o que reduz a margem de erro do DF. O DF para erro corresponde aos graus de liberdade restantes que não são usados no modelo.

Observação

Para um desenho fatorial de 2 níveis ou um desenho Plackett-Burman, se um experimento tiver pontos centrais, um DF é para o teste de curvatura. Se o termo para pontos centrais estiver no modelo, a linha para curvatura faz parte do modelo. Se o termo para pontos centrais não estiver no modelo, a linha para curvatura corresponde à parte do erro usada para testar os termos que estão no modelo. Em desenhos de superfície de resposta e desenhos de triagem definitiva é possível estimar os termos quadrados, de forma que o teste para a curva é desnecessário.

Dev. seq.

A desviância sequencial mede a desviância para diferentes componentes do modelo. Diferente da desviância ajustada, a desviância sequencial depende a ordem em que os termos são inseridos no modelo. Na tabela Desviância, o Minitab separa a desviância sequencial em diferentes componentes que descrevem a desviância explicada por diferentes fontes.

Modelo: A desviância sequencial para o modelo de regressão quantifica quanto da desviância total é explicada pelo modelo.

Termo: A desviância sequencial ajustada de um termo quantifica a diferença entre um modelo que logo antes e após incluir um termo em particular, com o termo e sem o termo.
Erro: A desviância sequencial do erro quantifica a desviância que o modelo não explica.
Total: A desviância sequencial ajustada total é a soma da desviância sequencial ajustada do modelo e a desviância sequencial ajustada do erro. A desviância sequencial ajustada total quantifica a desviância total nos dados.

Interpretação

Quando você especifica o uso da desviância sequencial para testes, o Minitab usa a desviância sequencial para calcular os valores-p para o modelo de regressão e os termos individuais. Normalmente, você interpreta os valores-p em vez da desviância sequencial.

Contribuição

A contribuição exibe a porcentagem que cada fonte na tabela de ANOVA contribui para o deviance sequencial total.

Interpretação

Porcentagens mais altas indicam que a fonte é responsável por mais do deviance na variável resposta. A contribuição do percentual do modelo de regressão é o mesmo que o R² deviance.

Dev. aj.

As desviâncias ajustadas são medidas de variação de diferentes componentes do modelo. A ordem dos preditores no modelo não afetam o cálculo das desviâncias ajustadas. Na tabela Desviâncias, o Minitab separa a desviância em diferentes componentes que descrevem a desviância explicada por diferentes fontes.

Modelo: A desviância ajustada do modelo de regressão quantifica a diferença entre o modelo atual e o modelo constante.
Termo: A desviância ajustada de um termo quantifica a diferença entre um modelo com o termo e o modelo sem o termo.
Erro: A desviância ajustada do erro quantifica a desviância que o modelo não explica.
Total: A desviância ajustada total é a soma da desviância ajustada do modelo e a desviância ajustada do erro. A desviância ajustada total quantifica a desviância total nos dados.

Interpretação

O Minitab usa as desviâncias ajustadas para calcular o valor-p de um termo. O Minitab também usa as desviâncias ajustadas para calcular a estatística R² da desviância. Normalmente, você interpreta os valores-p e a estatística R² em vez das desviâncias.

Média aj.

A desviância média ajustada mede quanta desviância um termo ou modelo explica para cada grau de liberdade. O cálculo da desviância média ajustada de cada termo supõe que todos os outros termos estejam no modelo.

Interpretação

O Minitab usa o valor do qui-quadrado para calcular o valor-p para um termo. Normalmente, você interpreta os valores-p em vez dos quadrados médios ajustados.

Qui-quadrado

Cada termo na tabela ANOVA têm um valor qui-quadrado. O valor qui-quadrado é a estatística de teste que determina se um termo ou modelo tem uma associação com a resposta.

Interpretação

O Minitab usa a estatística de teste para calcular o valor-p, que é usado para a tomada de uma decisão sobre a significância estatística dos termos e do modelo. O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula. Uma estatística qui-quadrado suficientemente grande resulta em um pequeno valor-p, que indica que o termo ou modelo é estatisticamente significativo.

Valor-p – Modelo

O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.

Interpretação

Para determinar se os dados oferecem evidências de que pelo menos um coeficiente no modelo de regressão é diferente de 0, compare o valor-p da regressão com o seu nível de significância para avaliar a hipótese nula. A hipótese nula para o valor-p para o modelo é de que todos os coeficientes de termos no modelo de regressão são 0. Em geral, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de se concluir que pelo menos um coeficiente seja diferente de 0, quando todos os coeficientes são 0.

Valor-p ≤ α: pelo menos um coeficiente é diferente de 0: Se o valor p for menor ou igual ao nível de significância, é possível concluir que pelo menos um coeficiente é diferente de 0.
Valor-p > α: não existe evidência suficiente para concluir que pelo menos um coeficiente é diferente de 0: Se o valor p for maior ou igual ao nível de significância, não é possível concluir que pelo menos um coeficiente seja diferente de 0. Talvez você deseje ajustar um novo modelo.

Os testes na tabela Deviance são testes da razão de verossimilhança. O teste na exibição expandida da tabela Coeficientes são os testes de aproximação Wald. Os testes da razão de verossimilhança são mais precisos para amostras pequenas do que os testes de aproximação Wald.

Valor-p – termo

O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.

Interpretação

Para determinar se a associação entre a resposta e cada termo no modelo é estatisticamente significativa, compare o valor-p para o termo com o seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula é que não há nenhuma associação entre o termo e a resposta. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de se concluir que existe uma associação quando não existe uma associação real.

Valor-p ≤ α: a associação é estatisticamente significativa: Se o valor-p for menor ou igual ao nível de significância, é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo.
Valor-p > α: a associação não é estatisticamente significativa: Se o valor-p for maior ou igual ao nível de significância, não é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo. Talvez seja necessário reajustar o modelo sem o termo.; Se houver vários preditores sem uma associação estatisticamente significativa com a resposta, você pode reduzir o modelo removendo os termos um de cada vez. Para obter mais informações sobre como remover os termos do modelo, vá para Redução de modelo.

Se um termo do modelo for estatisticamente significativo, a interpretação dependerá do tipo de termo. As interpretações são da seguinte maneira:

Se um fator contínuo for significativo, é possível concluir que o coeficiente para o fator é diferente de zero.
Se um fator categórico for significativo, é possível concluir que a probabilidade do evento não é a mesma para todos os níveis do fator.
Se um termo de interação for significativo, é possível concluir que a relação entre o fator e a probabilidade do evento depende de outros fatores no termo.
Se um termo quadrático é significativo, é possível concluir que a superfície de resposta possui curvatura.

Os testes na tabela Análise de variância são testes de razão de verossimilhança. O teste na exibição expandida da tabela Coeficientes são os testes de aproximação Wald. Os testes da razão de verossimilhança são mais precisos para amostras pequenas do que os testes de aproximação Wald.

Valor-p – Curvatura

O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.

O Minitab testa a curvatura quando o experimento tem pontos centrais. O teste examina a média ajustada da resposta nos pontos centrais em relação à média esperada se as relações entre os termos do modelo e a resposta são lineares. Para visualizar a curvatura, usegráficos fatoriais.

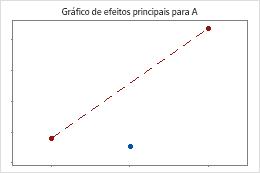
Os pontos centrais estão distantes da linha que une as médias dos pontos de extremidade, o que sugere uma relação curva. Utilize a valor-p para garantir que a curvatura seja estatisticamente significativa.

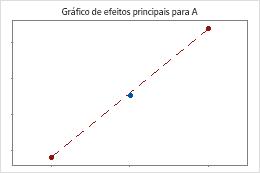
Os pontos centrais estão próximos à linha que une as médias dos pontos de extremidade. A curvatura provavelmente não é estatisticamente significativa.

Interpretação

Para determinar se pelo menos um dos fatores tem uma relação curva com a resposta, compare o valor-p da curvatura com seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula é aquela em que todas as relações entre os fatores e a resposta são lineares.

Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que diferentes condições entre os ensaios alteram a resposta quando as condições não alteram.

Valor-p ≤ α: pelo menos um fator tem uma relação curva com a resposta: Se o valor-p for menor ou igual ao nível de significância, é possível concluir que pelo menos um dos fatores tem uma relação curva de resposta. Talvez você queira adicionar pontos axiais ao experimento para poder modelar a curvatura.
Valor-p > α: não há evidências suficientes para concluir que há fatores que tenham uma relação de curva com a resposta: Se o valor-p for maior do que o nível de significância, não é possível concluir que algum dos fatores tem uma relação curva com a resposta. Se a curvatura é parte do modelo, é possível querer reajustar o modelo sem um termo para os pontos centrais de modo que a curvatura seja parte do erro.

Observação

Geralmente, se a curvatura não é estatisticamente significativa, você remove o termo do ponto central. Se você deixar os pontos centrais no modelo, o Minitab assume que o modelo contém a curvatura que o experimento fatorial não consegue ajustar. Devido ao ajuste inadequado, o Gráfico de Contornos, Gráfico de Superfície e Gráfico de Contornos Sobrepostos não estão disponíveis. Além disso, o Minitab não interpola entre os níveis de fator no experimento com Otimizador de Resposta. Para obter mais informações sobre maneiras de usar o modelo, acesse Visão geral do modelo armazenado.