Tukey é o método usado em ANOVA para criar intervalos de confiança para todas as diferenças pareadas entre as médias dos níveis dos fatores controlando a taxa de erro global para um nível de significância especificado. É importante considerar a taxa de erro global ao efetuar comparações múltiplas porque as chances de cometer um erro do tipo I para uma série de comparações é maior do que a taxa de erro para uma comparação separada. Para compensar essa alta taxa de erro, o método de Tukey ajusta o nível de confiança para cada intervalo individual de forma que o nível de confiança simultâneo resultante seja igual ao valor especificado.
Exemplos de intervalos de confiança de Tukey
Você está medindo os tempos de resposta de chips de memória. Você extrai uma amostra de 25 chips de cinco fabricantes diferentes.
Você decide para examinar todas os 10 comparações entre as cinco plantas para determinar especificamente quais médias são diferentes. Usando o método de Tukey, você especifica que todo o conjunto de comparações deve ter uma taxa de erro familiar de 0,05 (equivalente o nível de confiança simultâneo de 95%). O Minitab calcula que 10 os níveis de confiança individuais precisam ser de 99,35% para se obter o nível de confiança conjunto de 95%. Estes intervalos de confiança de Tukey mais amplos fornecem estimativas menos precisas do parâmetro da população, mas limitam a probabilidade de que um ou mais dos intervalos de confiança não contenham a diferença verdadeira para um máximo de 5%. Ao compreender este contexto, você pode então examinar os intervalos de confiança para determinar se algum não inclui zero, indicando uma diferença significativa.
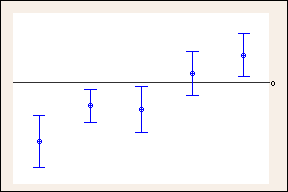
Intervalos de confiança com níveis de confiança individuais de 95%
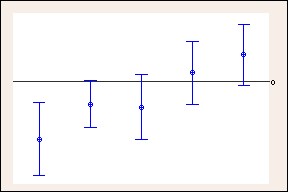
Intervalos de confiança com níveis de confiança individuais de 99,35% para obter um nível de confiança conjunto de 95% usando Tukey
Comparação entre intervalos de confiança de 95% e os intervalos de confiança mais largos usados por Tukey no exemplo anterior. A linha de referência em 0 mostra como os intervalos de confiança mais largos de Tukey podem mudar as conclusões. Intervalos de confiança contendo zero não denotam qualquer diferença. (Somente 5 das 10 comparações são mostradas por questões de espaço).
