O que é uma covariável?
Covariáveis são normalmente utilizadas na ANOVA e DOE. Nestes modelos, uma covariável é qualquer variável contínua, que geralmente não é controlada durante a coleta de dados. Com a inclusão de covariáveis, o modelo permite incluir e ajustar para variáveis de entrada que foram medidas, mas não aleatorizadas ou controladas no experimento. A adição de co-variáveis pode melhorar significativamente a precisão do modelo e pode afetar significativamente os resultados das análises finais. Incluindo uma covariável no modelo pode reduzir o erro no modelo para aumentar o poder dos testes de fatores. Covariáveis comuns incluem temperatura ambiente, umidade e características de uma peça ou sujeitos antes de um tratamento ser aplicado.
Por exemplo, um engenheiro quer estudar o nível de corrosão em quatro tipos de vigas de ferro. O engenheiro expõe cada feixe a um tratamento líquido para acelerar a corrosão, mas não pode controlar a temperatura do líquido. A temperatura é uma covariável que deve ser considerada no modelo.
Em um DOR, um engenheiro pode estar interessado no efeito da temperatura ambiente da covariável sobre o tempo de secagem de dois tipos diferentes de pintura.
Exemplo de adição de uma covariável a um modelo linear geral
A empresa têxtil usa três máquinas diferentes para a fabricação de fibras de monofilamento. Eles querem determinar se a resistência à ruptura da fibra varia de acordo com a máquina usada. Eles coletam dados sobre a força e diâmetro para 5 fibras selecionadas aleatoriamente a partir de cada máquina. Como a resistência das fibras está relacionada ao seu diâmetro, eles também registram o diâmetro da fibra para utilização como uma possível covariável.
| C1 | C2 | C3 |
|---|---|---|
| Máquina | Diâmetro | Resistência |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- Verifique se a covariável e a resposta se relacionam linearmente. Isso pode ser feito no Minitab analisando os dados com um gráfico de linha fixa.
- Selecione .
- Em Resposta(Y) insira Resistência.
- Em Preditor(X) insira Diâmetro.
- Avalie a proximidade dos dados para a linha ajustada e a proximidade de R2 de um "ajuste perfeito" (100%).
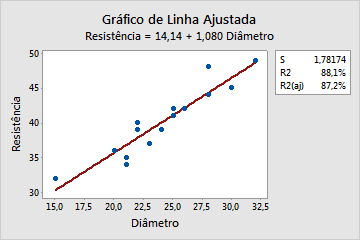
O gráfico de linha ajustada indica uma forte relação linear (87,2%) entre diâmetro e resistência.
- Faça a análise GLM com a covariável.
- Selecione .
- Em Respostas, insira Resistência.
- Em Fatores, insira Máquina.
- Em Covariáveis, insira Diâmetro.
- Clique em OK.
Para os dados de produção de fibras, o Minitab exibe os seguintes resultados:
Modelo Linear Generalizado: Resistência versus Diâmetro; Máquina
Análise de Variância Fonte GL SQ (Aj.) QM (Aj.) Valor F Valor-P Diâmetro 1 178,014 178,014 69,97 0,000 Máquina 2 13,284 6,642 2,61 0,118 Erro 11 27,986 2,544 Falta de ajuste 7 18,486 2,641 1,11 0,487 Erro puro 4 9,500 2,375 * * Total 14 346,400A estatística F para máquinas é 2,61 e o valor de p é 0,118. Como o valor de p > 0,05, você deixa de rejeitar a hipótese nula de que as resistências da fibra não variam com base na máquina usada no nível de significância de 5%. É possível assumir que as resistências da fibra são as mesmas em todas as máquinas. Observe que a estatística F para o diâmetro (covariável) é 69,97 com um valor de p de 0,000. Isto indica que o efeito da covariável é significativo. Isto é, o diâmetro tem um impacto estatisticamente significativo sobre a resistência da fibra.
Agora suponha que você execute a análise novamente omitindo a covariável. Isso gerará a seguinte saída:
Modelo Linear Generalizado: Resistência versus Máquina
Análise de Variância Fonte GL SQ (Aj.) QM (Aj.) Valor F Valor-P Máquina 2 140,4 70,20 4,09 0,044 Erro 12 206,0 17,17 Total 14 346,4Observe que a estatística F é 4,09 com um valor de p de 0,044. Sem a covariável no modelo, você rejeita a hipótese nula no nível de significância de 5% e conclui que a resistência das fibras varia em função da máquina usada.
Esta conclusão é completamente oposta à conclusão à qual você chega quando realiza a análise com a covariável. Este exemplo mostra como não incluir uma covariável pode produzir resultados equivocados da análise.
