Sobre a mensagem "deficiência de posto"
Os modelos lineares são postos completos quando há um número suficiente de observações por combinação de níveis de fator que sejam capazes de estimar todos os termos incluídos no modelo. Quando não há observações suficientes nos dados para ajustar o modelo, o Minitab remove os termos até que o modelo seja suficientemente pequeno para ser ajustado. É possível que outros modelos possam ajustar melhor os dados.
Suponha que você tenha um modelo GLM de dois fatores. Você tenta ajustar o modelo com termos A B e A*B e recebe um erro sobre "deficiência de posto". Isso indica que não há observações suficientes por combinação de nível de fator. Tente remover o termo de interação (A*B).
O que é deficiência de posto?
Deficiência de posto é uma condição que pode impedir o Minitab de efetuar cálculos com matrizes. Por exemplo, considere o conjunto de dados a seguir com duas variáveis preditoras e uma variável de resposta:
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | Y |
| 1,5 | 9,7 | 15,0 |
| 1,4 | 8,4 | 14,0 |
| 1,6 | 8,6 | 16,0 |
| 1,7 | 8,9 | 17,0 |
| 1,7 | 8,1 | 14,5 |
X1 e X2 são as variáveis preditoras, e Y é a variável de resposta. A análise de regressão no Minitab usa mínimos quadrados para calcular os coeficientes estimados b0, b1, b2, na seguinte equação linear:
Y = b0 + b1X1 + b2X2
O procedimento mínimos quadrados equivale a solucionar um conjunto de equações lineares.
b = (XTX)-1XTY
onde b é um vetor de coluna contendo os coeficientes estimados do modelo, X é uma matriz cuja primeira coluna é uma coluna de uns (usada para estimar a interceptação/constante) e cujas outras colunas são as colunas de dados preditores (X1, X2,…), e Y é o vetor de coluna de dados de resposta. Para o conjunto de dados anterior, as matrizes são:
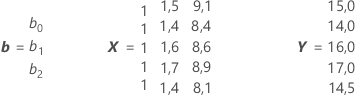
O Minitab usa a decomposição QR para calcular as estimativas dos parâmetros (b0, b1 e b2) e os desvios padrão dos parâmetros. O cálculo depende dos autovalores da matriz (XTX). Se alguns autovalores de (XTX) forem essencialmente zero, a matriz quadrada (XTX) é singular ou perto de ser singular, e o Minitab não será capaz de fazer os cálculos.
O que causa deficiência de posto?
Deficiência de posto ocorre se qualquer coluna de variáveis X pode ser expressa como uma combinação linear das outras colunas X. São mostrados dois exemplos usando C1, C2 e C3 como variáveis preditoras (X):
Exemplo 1
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 3 | 5 |
| 1,5 | 2,5 | 4 |
Exemplo 2
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 1,5 | 3 | 4 |
No primeiro exemplo, veja que C1 + C2 = C3.
No segundo exemplo, veja que 2*C1 = C2.
Se você tentar efetuar uma regressão (ou ANOVA) usando esses preditores, o Minitab removerá termos do modelo para efetuar a análise.
Deficiência de posto também pode ocorrer com dados categóricos:
Exemplo 3
| C1 | C2 | C3 |
|---|---|---|
| Máquina | Operador | Resposta |
| 1 | Joel | 15 |
| 1 | Joel | 18 |
| 1 | Joel | 17 |
| 2 | Bill | 14 |
| 2 | Bill | 15 |
| 2 | Bill | 16 |
Neste exemplo, observe que a coluna da máquina tem exatamente o mesmo padrão da coluna de operador. Se você executar a ANOVA com este conjunto de dados, o Minitab irá remover termos do modelo, a fim de realizar a análise.
- Um termo de interação incluído não têm, pelo menos, uma observação para cada combinação de níveis de fatores. Por exemplo, se A tem 3 níveis, B tem 4 níveis, e você inclui a interação A*B no modelo sem ter, pelo menos, uma observação para todas as 12 combinações dos níveis de fatores.
- Existe um aninhamento balanceado.
- Uma variável contínua no modelo não está especificada como covariável.
- Os graus de liberdade para Erro são negativos.
