Neste tópico
Etapa 1: Estimar o desvio padrão de cada população
Use os intervalos de confiança de Bonferroni para estimar o desvio padrão de cada população com base em seus fatores categóricos. Cada intervalo de confiança é uma gama de valores possíveis para o desvio padrão da população correspondente.
O Minitab ajusta os intervalos de confiança de Bonferroni para manter o nível de confiança em simultâneo. Com intervalos de confiança de Bonferroni de 95%, é possível ter 95% de certeza de que todo o conjunto de intervalos de confiança inclui os verdadeiros desvios padrão da população para todos os grupos.
Controlar o nível de confiança simultâneo é particularmente importante quando você realiza várias comparações. Se você não controlar o nível de confiança simultâneo, a probabilidade de que pelo menos um intervalo de confiança não contenha o desvio padrão verdadeiro, aumenta com o número de intervalos de confiança.
Observação
Não é possível usar os intervalos de confiança de Bonferroni para determinar se as diferenças entre os pares de grupos são estatisticamente significativas. Para determinar a significância estatística das diferenças entre os pares de grupos, use os intervalos de comparações múltiplas na etapa 2.
Para obter mais informações, acesse Uso de níveis de confiança para identificar diferenças significativas entre níveis de fatores em comparações múltiplas e O que é o método de Bonferroni?.
Método
| Hipótese nula | Todas as variâncias são iguais |
|---|---|
| Hipótese alternativa | No mínimo uma variância é diferente |
| Nível de significância | α = 0,05 |
Intervalos de 95% de Confiança Bonferroni para os Desvios Padrão
| Fertilizante | N | DesvPad | IC |
|---|---|---|---|
| GrowFast | 50 | 4,28743 | (3,43659; 5,61790) |
| Nenhum | 50 | 5,09137 | (4,24793; 6,40914) |
| SuperPlant | 49 | 5,49969 | (4,48577; 7,08914) |
Principais resultados: StDev, Intervalos de confiança de Bonferroni de 95%, Nível de confiança individual
Nestes resultados, os intervalos de confiança de Bonferroni indicam que é possível ter 95% de certeza de que todo o conjunto de intervalos de confiança inclui os verdadeiros desvios padrão da população para todos os grupos. Além disso, o nível de confiança individual indica o grau de confiança que é possível ter de que um intervalo de confiança individual contenha o desvio padrão da população desse grupo específico. Por exemplo, é possível ter 98,3333% de confiança de que o desvio padrão para a população do GrowFast esteja dentro do intervalo de confiança (3,43659, 5,61790).
Etapa 2: Determinar se os desvios padrão da população são estatisticamente diferentes
Utilize o gráfico de resumo para determinar se alguma das diferenças entre os desvios padrão é estatisticamente significativa. Os tipos de testes e os intervalos que o Minitab exibe dependem se você marcou Usar teste com base na distribuição normal na subcaixa de diálogo Opções e no número de grupos em seus dados.
- Valores-p para os testes
-
Utilize os valores-p no gráfico de resumo para determinar se alguma das diferenças entre os desvios padrão é estatisticamente significativa. O Minitab exibe os resultados de um ou dois testes que avaliam a igualdade de variâncias. Se você tiver dois valores-p e eles discordarem, acesse Todas as estatísticas e gráficos e clique em "Testes" para obter informações sobre qual teste de usar.
Compare o valor-p com seu nível de significância para avaliar a hipótese nula. A hipótese nula afirma que os desvios padrão do grupo são todos iguais. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica que o risco de se concluir que existe uma diferença, quando, na verdade, não existe nenhuma diferença real, é de 5%.
Use as seguintes orientações para interpretar os valores-p:- Se o valor-p for > α, as diferenças entre os desvios padrão não são estatisticamente significativas.
- Se o valor-p for ≤ α: as diferenças entre alguns dos desvios padrão não são estatisticamente significativas.
- Intervalos de comparação múltiplos
-
Se você não selecionou Usar teste com base na distribuição normal, o gráfico de resumo exibe os intervalos de confiança para o método de múltiplas comparações. Em geral, você pode basear suas conclusões sobre o teste de múltiplas comparações e os intervalos de múltiplas comparações, a menos que você tenha pequenas amostras de distribuições muito assimétricas ou com caudas pesadas.
Use os intervalos de múltiplas comparações para identificar pares específicos de desvios padrão que não são iguais. Se dois intervalos não se sobrepuserem, a diferença entre os respectivos desvios padrão é estatisticamente significativa. Se o valor-p para o teste de múltiplas comparações for menor do que o seu nível de significância, pelo menos um par de intervalos não se sobrepõe.
- Intervalos de confiança de Bonferroni
-
Se você selecionou Usar teste com base na distribuição normal, o gráfico de resumo apresenta os intervalos de confiança de Bonferroni para estimar o desvio padrão de cada população. Não é possível usar esses intervalos para determinar se as diferenças entre os pares de grupos são estatisticamente significativas. Vá para a etapa 1 para obter mais informações sobre como interpretar os intervalos de confiança de Bonferroni.
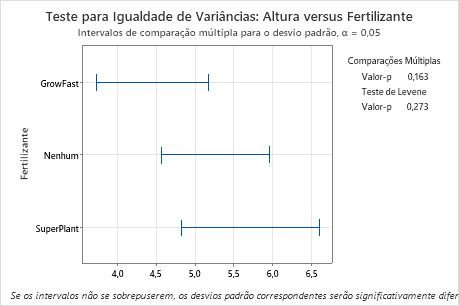
Principais resultados: múltiplas comparações, valor-p
Neste gráfico de resumo, o valor p para o teste de múltiplas comparações é maior do que o nível de significância de 0,05. Nenhuma das diferenças entre os grupos é estatisticamente significativa, e todos os intervalos de comparações sobrepõem.
