Neste tópico
Hipótese nula, hipótese alternativa
O teste de igualdade de variâncias é um teste de hipóteses que avalia duas afirmações mutuamente exclusivas relacionadas a dois ou mais desvios padrão da população. Estas duas afirmações são chamadas de hipótese nula e hipótese alternativa. Um teste de hipótese usa dados amostrais para determinar se deve rejeitar a hipótese nula.
- Hipótese nula (H0)
- A hipótese nula afirma que os desvios padrão da população são todos iguais.
- Hipótese Alternativa (HA)
- A hipótese alternativa afirma que nem todos os desvios padrão da população são iguais.
Interpretação
Compare o valor de p com o nível de significância para decidir se deve rejeitar ou deixar de rejeitar a hipótese nula.
N
O tamanho amostral (N) é o número total de observações em cada grupo.
Interpretação
O tamanho amostral afeta o intervalo de confiança e o poder do teste.
Normalmente, uma amostra maior produz um intervalo de confiança mais estreito. Uma amostra maior também proporciona ao teste mais poder para detectar uma diferença.
Desvio padrão (StDev)
O desvio padrão é a medida mais comum de dispersão, ou quão dispersos os dados estão da média. O símbolo σ (sigma) é muitas vezes usado para representar o desvio padrão da população. O símbolo s é usado para representar o desvio padrão de uma amostra.
Interpretação
O desvio padrão usa as mesmas unidades que a variável. Um valor de desvio padrão mais alto indica maior dispersão nos dados. Uma orientação para os dados que seguem uma distribuição normal é que aproximadamente 68% dos valores estão dentro de um desvio padrão da média, 95% dos valores estão dentro de dois desvios padrão e 99,7% dos valores estão dentro de três desvios padrão.
Intervalos de confiança de Bonferroni
Use os intervalos de confiança de Bonferroni para estimar o desvio padrão de cada população com base em seus fatores categóricos. Cada intervalo de confiança é uma faixa de valores possíveis que tende a conter o desvio padrão da população correspondente. O Minitab ajusta os intervalos de confiança de Bonferroni para manter o nível de confiança em simultâneo.
Controlar o nível de confiança simultâneo é particularmente importante quando você avalia intervalos de múltiplas comparações. Se você não controlar o nível de confiança simultâneo, a probabilidade de que pelo menos um intervalo de confiança não contenha o desvio padrão verdadeiro, aumenta com o número de intervalos de confiança.
Para obter mais informações, acesse Compreendendo os níveis de confiança individuais e simultâneos em múltiplas comparações e O que é o método Bonferroni?
Observação
Não é possível usar os intervalos de confiança de Bonferroni para determinar se as diferenças entre os pares de grupos são estatisticamente significativas. Use os valores de p e os intervalos de confiança de múltiplas comparações no gráfico de resumo para determinar a significância estatística das diferenças.
Interpretação
Método
| Hipótese nula | Todas as variâncias são iguais |
|---|---|
| Hipótese alternativa | No mínimo uma variância é diferente |
| Nível de significância | α = 0,05 |
Intervalos de 95% de Confiança Bonferroni para os Desvios Padrão
| Fertilizante | N | DesvPad | IC |
|---|---|---|---|
| GrowFast | 50 | 4,28743 | (3,43659; 5,61790) |
| Nenhum | 50 | 5,09137 | (4,24793; 6,40914) |
| SuperPlant | 49 | 5,49969 | (4,48577; 7,08914) |
Nestes resultados, os intervalos de confiança de Bonferroni de 95% indicam que é possível ter 95% de confiança de que todo o conjunto de intervalos de confiança inclui os verdadeiros desvios padrão da população para todos os grupos. Além disso, o nível de confiança individual indica o grau de confiança que é possível ter de que um intervalo de confiança individual contenha o desvio padrão da população desse grupo específico. Por exemplo, é possível ter 98,3333% de confiança de que o desvio padrão para a população do GrowFast esteja dentro do intervalo de confiança (3,43659, 5,61790).
Nível de confiança individual
O nível de confiança individual é a porcentagem de vezes que um único intervalo de confiança inclui o verdadeiro desvio padrão para esse grupo específico se você repetir o estudo várias vezes.
À medida que aumenta o número de intervalos de confiança em um conjunto, a probabilidade de que pelo menos um intervalo de confiança não conter os verdadeiros desvio padrão aumenta. O nível de confiança simultâneo indica o grau de confiança você pode ter de que todo o conjunto de intervalos de confiança inclua os verdadeiros desvios padrão da população para todos os grupos.
Interpretação
Método
| Hipótese nula | Todas as variâncias são iguais |
|---|---|
| Hipótese alternativa | No mínimo uma variância é diferente |
| Nível de significância | α = 0,05 |
Intervalos de 95% de Confiança Bonferroni para os Desvios Padrão
| Fertilizante | N | DesvPad | IC |
|---|---|---|---|
| GrowFast | 50 | 4,28743 | (3,43659; 5,61790) |
| Nenhum | 50 | 5,09137 | (4,24793; 6,40914) |
| SuperPlant | 49 | 5,49969 | (4,48577; 7,08914) |
Você pode ter 98,3333% de confiança de que cada intervalo de confiança individuas contém o desvio padrão da população para esse grupo específico. Por exemplo, é possível ter 98,3333% de confiança de que o desvio padrão para a população do GrowFast esteja dentro do intervalo de confiança (3,43659, 5,61790). No entanto, como o conjunto inclui três intervalos de confiança, você pode ter apenas 95% de confiança de que todos os intervalos contêm os valores verdadeiros.
Testes
Os tipos de testes de igualdade de variâncias que o Minitab exibe dependem se você selecionou Usar teste com base na distribuição normal na subcaixa de diálogo de Opções e o número de grupos em seus dados.
Múltiplas comparações, métodos de Levene
Se você não selecionou Usar teste com base na distribuição normal, o Minitab exibe resultados de teste para o método de comparações múltiplas e para o método de Levene. Para distribuições mais contínuas, os dois métodos fornecem uma taxa de erro tipo 1 próxima do nível de significância especificado (denotado como alfa). O método de múltiplas comparações é geralmente mais poderoso. Se o valor p para o método de múltiplas comparações for significante, você poderá usar o gráfico de sumário para identificar populações específicas com desvios padrão diferentes entre si.
- Cada uma de suas amostras tem menos de 20 observações.
- A distribuição para uma ou mais das populações é extremamente assimétrica ou tem caudas pesadas. Em comparação com a distribuição normal, uma distribuição com caudas pesadas tem mais dados nas suas extremidades inferiores e superiores.
Se o valor de p para o teste de múltiplas comparações for menor do que o seu nível de significância escolhido, as diferenças entre alguns dos desvios padrão são estatisticamente significativas. Use os intervalos de múltipla comparação para determinar quais desvios padrão são significativamente diferentes uns dos outros. Se dois intervalos não se sobrepõem, então os desvios padrão correspondentes (e as variâncias) são significativamente diferentes.
Quando você tem pequenas amostras de distribuições muito assimétricas ou com caudas pesadas, a taxa de erro tipo I para o método de múltiplas comparações pode ser maior do que α. Sob estas condições, se o método de Levene proporcionar um valor de p menor do que o método de múltiplas comparações, baseie suas conclusões no método de Levene.
Teste F, teste de Bartlett
Se você selecionar Usar teste com base na distribuição normal e você tem dois grupos, o Minitab executa o teste F. Se você tem 3 grupos ou mais, o Minitab executa o teste de Bartlett.
O teste F e teste de Bartlett são precisos apenas para dados normalmente distribuídos. Qualquer desvio da normalidade pode fazer com que estes testes para produzam resultados imprecisos. No entanto, se os dados estão em conformidade com uma distribuição normal, o teste F e o teste de Bartlett são tipicamente mais poderosos do que o método de comparações múltiplas ou o método de Levene.
Se o valor de p para o teste for menor do que o seu nível de significância escolhido, as diferenças entre alguns dos desvios padrão são estatisticamente significativas.
Estatística de teste
Observação
O teste de múltiplas comparações não usa uma estatística de teste.
Interpretação
O Minitab usa a estatística de teste para calcular o valor de p, que é usado para a tomada de uma decisão sobre a significância estatística das diferenças entre os desvios padrão. O valor de p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
A estatística de teste suficientemente elevada indica que a diferença entre alguns dos desvios padrão é estatisticamente significativa.
Você pode usar a estatística de teste para determinar se deve rejeitar a hipótese nula. No entanto, o valor de p é usado mais frequentemente porque é mais fácil de ser interpretado.
Valor de p
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Interpretação
Utilize o valor de p para determinar se alguma diferença entre os desvios padrão é estatisticamente significativo. O Minitab exibe os resultados de um ou dois testes que avaliam a igualdade de variâncias. Se você tiver dois valores de p e eles discordarem, consulte "Testes".
Para determinar se alguma das diferenças entre os desvios padrão é estatisticamente significativa, compare o valor de p com o seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula afirma que as médias do grupo são todas iguais. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica que o risco de se concluir que existe uma diferença, quando, na verdade, não existe nenhuma diferença real, é de 5%.
- Se o valor de p for > α: as diferenças entre os desvios padrão não são estatisticamente significativas.
- Se o valor de p for ≤ α: as diferenças entre alguns dos desvios padrão não são estatisticamente significativas.
Gráfico de resumo
O gráfico de resumo mostra os valores-p e os intervalos de confiança para os testes de igualdade de variâncias. Os tipos de testes e os intervalos que o Minitab exibe dependem se você selecionou Usar teste com base na distribuição normal na caixa de diálogo Opções e no número de grupos em seus dados.
Se você não selecionou Usar teste com base na distribuição normal, o gráfico de resumo exibe os valores-p, tanto para o método de múltiplas comparações como para o método de Levene. O gráfico também exibe intervalos de múltipla comparação. Você deve optar entre os dois métodos baseados nas propriedades dos seus dados.
Se você selecionou Usar teste com base na distribuição normal e tem dois grupos, o Minitab executa o teste F. Se você tiver 3 ou mais grupos, o Minitab realizará o teste de Bartlett. Para qualquer destes testes, o gráfico também exibe intervalos de confiança de Bonferroni.
Valores-p
O valor-p é uma probabilidade que mede a evidência contra a hipótese nula. As probabilidades inferiores fornecem evidências mais fortes contra a hipótese nula.
Utilize os valores-p para determinar se alguma diferença entre os desvios padrão é estatisticamente significativo. O Minitab exibe os resultados de um ou dois testes que avaliam a igualdade de variâncias. Se você tiver dois valores-p e eles discordam, consulte a seção sobre testes para obter informações sobre qual teste deve ser usado.
Para determinar se alguma das diferenças entre os desvios padrão é estatisticamente significativa, compare o valor-p com o seu nível de significância a fim de avaliar a hipótese nula. A hipótese nula afirma que os desvios padrão do grupo são todos iguais. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica que o risco de se concluir que existe uma diferença, quando, na verdade, não existe nenhuma diferença real, é de 5%.
- Se o valor-p for > α, as diferenças entre os desvios padrão não são estatisticamente significativas.
- Se o valor-p for ≤ α: as diferenças entre alguns dos desvios padrão não são estatisticamente significativas.
Intervalos de comparação múltiplos
Se você não selecionou Usar teste com base na distribuição normal, o gráfico de resumo exibe intervalos de múltipla comparação.
Se for válido para você usar o valor-p da múltipla comparação, é possível usar os intervalos de confiança da múltipla comparação para identificar pares específicos de grupos que tenham uma diferença que seja estatisticamente significativa. Se dois intervalos não se sobrepuserem, a diferença entre os respectivos desvios padrão é estatisticamente significativa.
Se as propriedades de seus dados exigem que você use o método de Levene, não avalie os intervalos de confiança no gráfico de resumo.
Intervalos de confiança de Bonferroni
Se você selecionou Usar teste com base na distribuição normal, o gráfico de resumo apresenta os intervalos de confiança de Bonferroni.
Use os intervalos de confiança de Bonferroni para estimar o desvio padrão de cada população para seus fatores categóricos. Cada intervalo de confiança é uma faixa de valores possíveis para o desvio padrão da população correspondente. O Minitab ajusta os intervalos de confiança de Bonferroni para controlar o nível de confiança simultâneo.
Controlar o nível de confiança simultâneo é particularmente importante quando você avalia intervalos de múltiplas comparações. Se você não controlar o nível de confiança simultâneo, a probabilidade de que pelo menos um intervalo de confiança não contenha o desvio padrão verdadeiro, aumenta com o número de intervalos de confiança.
Para obter mais informações, acesse Compreendendo os níveis de confiança individuais e simultâneos em múltiplas comparações e O que é o método Bonferroni?
Observação
Não é possível usar os intervalos de confiança de Bonferroni para determinar se as diferenças entre os pares de grupos são estatisticamente significativas. Use os valores-p e os intervalos de confiança de múltiplas comparações no gráfico de resumo para determinar a significância estatística das diferenças.
Interpretação
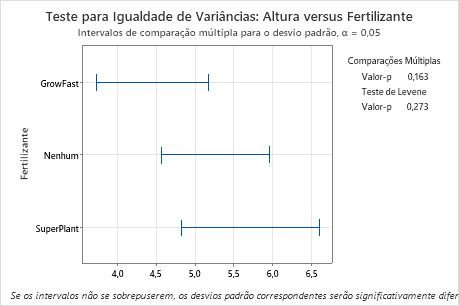
Neste gráfico de resumo, o valor p para o teste de múltiplas comparações é mais elevado do que o nível de significância de 0,05. Nenhuma das diferenças entre os grupos é estatisticamente significativa, e todos os intervalos de múltiplas comparações sobrepõem.
Gráfico de valores individuais
Um gráfico de valores individuais exibe os valores individuais em cada amostra. Um gráfico de valores individuais facilita a comparação das amostras. Cada círculo representa uma observação. Um gráfico de valores individuais é especialmente útil quando o tamanho da amostra é pequeno.
Interpretação
Use um gráfico de valores individuais para examinar a dispersão dos dados e identificar quaisquer outliers potenciais. Os gráficos de valores individuais são melhores quando o tamanho amostral é menor do que 50.
- Dados Assimétricos
-
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos. Quando os dados são assimétricos, a maior parte dos dados está localizada no lado alto ou baixo do gráfico. Dados assimétricos indicam que os dados podem não estar normalmente distribuídos. Muitas vezes, a assimetria é mais fácil de ser detectada com um gráfico de valores individuais, um histograma ou um boxplot.
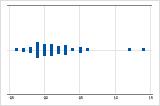
Assimétricos à direita
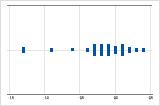
Assimétricos à esquerda
Por exemplo, o gráfico de valores individuais com dados assimétricos à direita mostra os tempos de espera. A maioria dos tempos de espera são relativamente curtos e apenas alguns tempos de espera são mais longos. O gráfico de valores individuais com dados assimétricos à esquerda mostra os dados de tempos de falhas. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
- Outliers
-
Outliers, que são valores de dados que estão distantes dos outros valores de dados, podem afetar fortemente os resultados da análise. Muitas vezes, os outliers são fáceis de identificar em um gráfico de valores individuais.
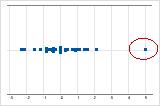
Em um gráfico de valores individuais, valores de dados anormalmente altos ou baixos indicam outliers potenciais.
Tente identificar a causa de qualquer outliers. Corrija todos os erros de entrada de dados ou de medição. Considere remover valores de dados que estejam associados a eventos anormais, que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
Boxplot
O boxplot fornece um resumo gráfico da distribuição de uma amostra. O boxplot facilita a comparação da forma, da tendência central e da variabilidade das amostras.
Interpretação
Use um boxplot para examinar a dispersão dos dados e identificar quaisquer outliers potenciais. Os boxplots são melhores quando o tamanho amostral é maior do que 20.
- Dados Assimétricos
-
Examine a dispersão de seus dados para determinar se eles parecem ser assimétricos. Quando os dados são assimétricos, a maior parte dos dados está localizada no lado alto ou baixo do gráfico. Dados assimétricos indicam que os dados podem estar normalmente distribuídos. Muitas vezes, a assimetria é mais fácil de ser detectada com um gráfico de valores individuais, um histograma ou um boxplot.
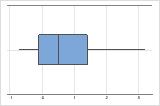
Assimétricos à direita
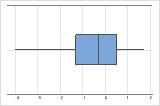
Assimétricos à esquerda
O boxplot com dados assimétricos à direita mostra os tempos de espera médios. A maioria dos tempos de espera são relativamente curtos, e somente alguns dos tempos de espera são mais longos. O boxplot com dados assimétricos à esquerda mostra os dados de taxa de falha. Alguns itens falham imediatamente e muitos outros itens falham posteriormente.
Os dados que são fortemente assimétricos podem afetar a validade do valor de p se a amostra for pequena (< 20 valores). Se seus dados forem severamente assimétricos e você tiver uma pequena amostra, considere aumentar o tamanho amostral.
- Outliers
-
Outliers, que são valores de dados distantes dos outros valores de dados, podem afetar fortemente os resultados da análise. Frequentemente, os outliers são facilmente identificados em um boxplot.
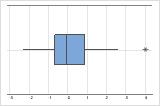
Em um boxplot, os asteriscos (*) identificam outliers.
Tente identificar a causa de qualquer outliers. Corrija todos os erros de entrada de dados ou de medição. Considere remover valores de dados que estejam associados a eventos anormais, que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
