Métodos e fórmulas para as estatísticas condicionais em Predição para Ajustar modelo de efeitos mistos

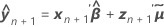
Notação

Termo	Descrição
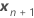	o vetor de novas configurações para os termos de efeitos fixos
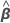	os coeficientes estimados para os termos de efeitos fixos
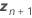	O vetor de novas configurações para os termos de efeitos aleatórios
	As predições de BLUP para os termos de efeito aleatório

O erro padrão de um valor ajustado condicional é igual à raiz quadrada da expressão de variância a seguir.

onde

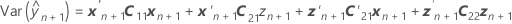
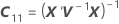
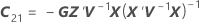
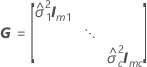
X é a matriz de experimento para os termos de efeitos fixos e Z é a matriz de projeto para os termos de efeitos aleatórios.

A amplitude na qual espera-se que a resposta média de um dado conjunto de valores do preditor caia.

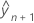é o ajuste condicional. 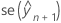o erro padrão do ajuste.

Os graus de liberdade utilizam esta fórmula para o caso condicional:

onde

e

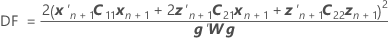
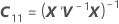
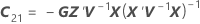
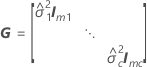
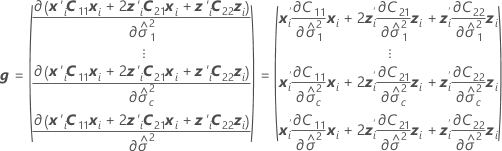
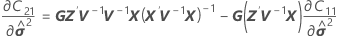
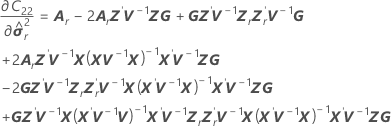
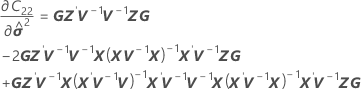
Notação

Termo	Descrição
W	a matriz de variância-covariância assintótica de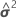

Para mais detalhes sobre a notação, acesse Ajuste e Resíduos Condicionais em in Modelo de Efeitos Mistos de Ajuste.

O intervalo de predição condicional é:

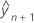é o ajuste condicional em todas as configurações de novas variáveis.

=

=

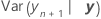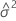
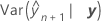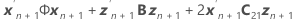
Os graus de liberdade utilizam esta fórmula para o caso condicional:

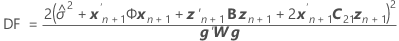
em que

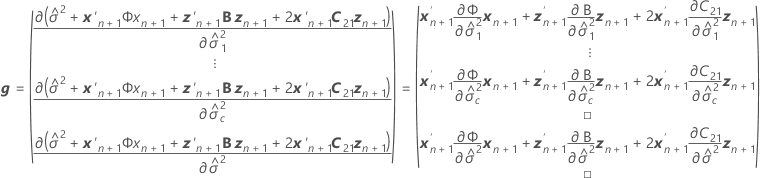
Notação

Termo	Descrição
W	a matriz de variância-covariância assintótica das estimativas do componente de variância
I	a matriz de identidade
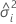	o componente de variância para o io termo de efeito aleatório
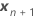	o vetor de novas configurações para os termos de efeitos fixos
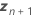	o vetor de novas configurações para os termos de efeitos aleatórios
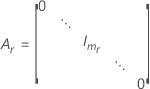
c	o número de termos aleatórios no modelo
B
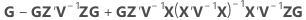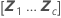C21
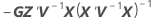G
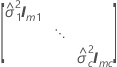mi	o número de níveis para o efeito aleatório
X	a matriz de experimento n x p para os termos de efeitos fixos,
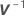	inverso da matriz de variância-covariância
	a matriz de experimento n x mi para o termo aleatório no modelo