Métodos e fórmulas para várias comparações em ANOVA com 1 fator

O Minitab oferece cinco métodos diferentes para comparar várias médias de fator na análise de variância com um fator: de Tukey, de Fisher, de Dunnett, MCB de Hsu Games-Howell. As fórmulas para estes testes estão relacionadas abaixo.

Notação

Termo	Descrição
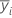	média de amostras para o i o nível de fator
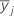	a média de amostras para o jo nível de fator
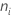	o número de observações no nível i
r	o número de níveis
s	o desvio padrão combinado ou sqrt(MSE)
u	os graus de liberdade para erro
α	a probabilidade simultânea de cometer um erro de Tipo I
α*	a probabilidade individual de cometer um erro Tipo I

Tukey:

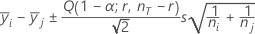
onde Q = percentil α superior da distribuição da variedade estudentizada com r e n_T - r graus de liberdade.

Para determinar a taxa de erro individual a partir da taxa de erro simultânea, utilize a seguinte fórmula:

Fisher:

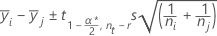
onde t = ponto α/2 superior da distribuição t de Student com u graus de liberdade.

Para determinar a o nível de confiança simultâneo partir da taxa de erro individual, utilize a seguinte fórmula:

Dunnett:

Para ver como d é calculado, consulte a página 63 em Hsu¹.

MCB de Hsu:

Fornecemos fórmulas para o caso em que todos os tamanhos de grupo são iguais a n. Fórmulas para tamanhos de grupos diferentes são encontradas em Hsu¹. Suponha que você tenha escolhido o melhor para ser a maior média, e queira o intervalo de confiança para a i^a média menos o maior dos outros.

O ponto de extremidade inferior e menor do que zero e

O ponto de extremidade superior e maior do que zero e

Para ver como d é calculado, consulte a página 83 em Hsu¹.

Quando o melhor é a menor das médias de nível, as fórmulas são as mesmas, exceto que max é substituído por min.

Teste de Games-Howell e Welch

A estatística de teste de Welch é computada da seguinte maneira.

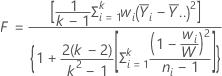
O valor de p para o teste de Welch é uma probabilidade da cauda superior para uma distribuição F com graus de liberdade do numerador k - 1, onde k é o número de níveis de X, e os graus de liberdade do denominador dados por:

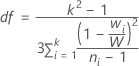
O intervalo de comparação para μ_i - μ_j is

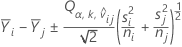
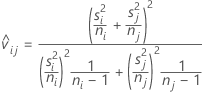
A razão-t usada para calcular o valor de P ajustado é igual a:

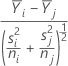
Onde:

A j^a resposta no i^o nível do fator categórico é igual a:

Y_ij, j = 1, ... , n_i; i = 1, ... k

A resposta média no i^o nível é igual a:

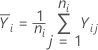
A variância da amostra é igual a

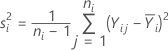
O peso para o nível i é igual a:

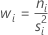
A soma de todos os pesos é igual a:

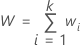
A média ponderada global de respostas é igual a:

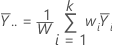
Agradecimentos

Estamos muito gratos pela assistência na concepção e implementação de várias comparações de Jason C. Hsu.

[1] J.C. Hsu (1996). Multiple Comparisons, Theory and methods. Chapman & Hall.