Neste tópico
Notação
A notação é fundamental para a compreensão de modelos de ANOVA. Segue-se a notação usada pela análise de variância com um fator.
| Termo | Descrição |
|---|---|
| r | número de níveis do fator, i = 1 ...r |
| i | um determinado nível de fator |
| j | um determinado caso para um nível de fator específico, j = 1 ...ni |
| yij | jo observação da resposta para o io nível de fator |
| ni | número de observações para o io nível de fator |
| nT | número total de casos |
| μi | média real de observações no io nível de fator |
| yi. | total de observações no io nível de fator |
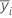 | média da resposta para o io fator |
Ajuste de modelo
Fórmula
O modelo de análise de variância com um fator pode ser especificado de várias maneiras. O modelo com médias por célula é:
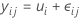
Todas as observações para o nível de fator têm a mesma expectativa, μi. Como μi é uma constante, todas as observações têm a mesma variância, independentemente do nível de fator.
Na análise de variância, a estimativa de mínimos quadrados é usada para ajustar o modelo e fornecer estimativas para os parâmetros, μi.
O teste de hipótese para a análise de variância com um fator é:
H0: μ1 = μ2= … = μr
H1: Pelo menos uma média não é igual às outras
Notação
| Termo | Descrição |
|---|---|
| μi | parâmetros ou a média verdadeira de observações no io nível de fator |
| εij | erro que é independente e normalmente distribuído com média 0 e variância constante σ2 |
