Neste tópico
Graus de liberdade (DF)
Fórmula
- DF (Fator) = r – 1
- DF Erro = nT – r
- Total = nT – 1
Notação
| Termo | Descrição |
|---|---|
| nT | número de observações total |
| r | número de níveis de fator |
Soma de quadrados (SS)
Fórmula
A soma das distâncias ao quadrado. SS total é a variação total nos dados. SS (Fator) é o desvio da média do nível de fator estimado em torno da média global. Também é conhecido como a soma dos quadrados entre tratamentos. SS Erro é o desvio de uma observação a partir de sua média de nível de fator correspondente. Também é conhecido como erro dentro de tratamentos.
Os cálculos são:

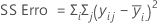
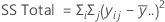
Notação
| Termo | Descrição |
|---|---|
| y̅i. | média de observações no io nível de fator |
| y̅.. | média de todas as observações |
| yij | valor da ja observação no io nível de fator |
Quadrados médios (MS)
Fórmula
O cálculo para o quadrado médio para o fator seguinte:

O cálculo para o quadrado médio de erro a seguir:

Notação
| Termo | Descrição |
|---|---|
| MS | Quadrado Médio |
| SS | Soma dos Quadrados |
| DF | Graus de liberdade |
Valor F
Fórmula

Os graus de liberdade para o numerador são r – 1. Os graus de liberdade para o denominador são nT – r.
Notação
| Termo | Descrição |
|---|---|
| nT | número de observações total |
| r | número de níveis de fator |
Valor de p
Os valores de p são usados em testes de hipóteses para ajudá-lo a decidir se deve rejeitar ou não uma hipótese nula. O valor de p é a probabilidade de se obter uma estatística de teste que seja pelo menos tão extrema quanto o valor calculado real, se a hipótese nula for verdadeira. Um valor de corte normalmente utilizado para o valor de p é 0,05. Por exemplo, se o valor de p calculado de uma estatística de teste for inferior a 0,05, você deve rejeitar a hipótese nula.
S
Uma estimativa de σ, a medida do desvio padrão dentro de uma amostra. Observe que para S2 = MP Erro. Isto é equivalente ao desvio padrão combinado utilizado no cálculo dos intervalos de confiança individuais.
R2


R2 também pode ser calculado como a correlação ao quadrado de y e 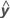 .
.
Notação
| Termo | Descrição |
|---|---|
| SS | Soma dos Quadrados |
| y | variável de resposta |
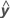 | variável de resposta ajustada |
R2 (aj)

Notação
| Termo | Descrição |
|---|---|
| MS | Quadrado Médio |
| SS | Soma dos Quadrados |
| DF | Graus de liberdade |
R2 (pred)
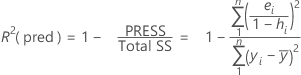
Enquanto os cálculos para R2(pred) podem produzir valores negativos, o Minitab exibe zero para estes casos.
Notação
| Termo | Descrição |
|---|---|
| yi | i o valor de resposta observada |
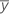 | resposta média |
| n | número de observações |
| ei | i o resíduo |
| hi | i o elemento diagonal de X(X'X)–1X' |
| X | matriz do experimento |
